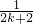摘要：设f(n)=(1+,用数学归纳法证明f(n)≥3.在“假设n=k时成立 后.f(k+1)与f(k)的关系是f(k+1)=f(k)· .
网址：http://m.1010jiajiao.com/timu3_id_4470389[举报]
在用数学归纳法证明f（n）=
+
+…+
＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
查看习题详情和答案>>
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
A．
| B．
| ||||||||||
C．
| D．
|
在用数学归纳法证明f（n）=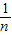
+
+…+
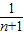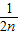＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
A．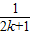
+
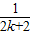
B．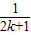
+
-
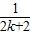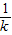
C．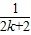
-
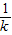
D．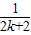
-
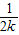
查看习题详情和答案>>
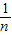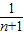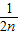++…+＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）A．
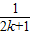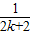
+B．
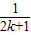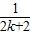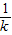
+-C．
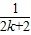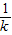
-D．
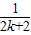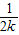
-查看习题详情和答案>>
在用数学归纳法证明f（n）=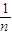
+
+…+
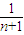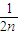＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）
A．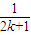
+
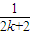
B．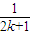
+
-
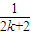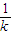
C．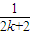
-
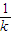
D．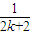
-
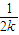
查看习题详情和答案>>
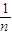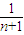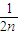++…+＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）A．
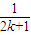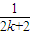
+B．
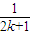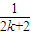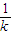
+-C．
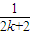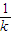
-D．
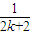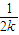
-查看习题详情和答案>>
+
+…+
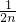＜1（n∈N*，n≥3）的过程中：假设当n=k（k∈N*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=
+
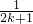