摘要:21.已知有穷数列共有2项(整数≥2).首项=2.设该数列的前项和为.且=+2(=1.2.┅.2-1).其中常数>1. (1)求证:数列是等比数列, (2)若=2.数列满足=(=1.2.┅.2).求数列的通项公式, 中的数列满足不等式|-|+|-|+┅+|-|+|-|≤4.求的值. 解:(1).则.两式相减.得. (又) ∴数列是首项为.公比为的等比数列. (2)=.(=1.2.┅.2). 知.数列是首项为.公差为的等差数列. 又.∴时.,时.. ∴|-|+|-|+┅+|-|+|-| .
网址:http://m.1010jiajiao.com/timu3_id_4469539[举报]
21.已知有穷数列

 共有2
共有2 项(整数
项(整数 ≥2),首项
≥2),首项 =2.设该数列的前
=2.设该数列的前 项和为
项和为 ,且
,且 =
=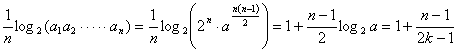 +2(
+2( =1,2,┅,2
=1,2,┅,2 -1),其中常数
-1),其中常数 >1.
>1.
(1)求证:数列![]()
![]()
![]() 是等比数列;
是等比数列;
(2)若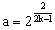 ,数列
,数列![]()
![]()
![]() 满足
满足![]() =
=![]() (
(![]() =1,2,┅,2
=1,2,┅,2![]() ),求数列
),求数列![]()
![]()
![]() 的通项公式;
的通项公式;
(3)若(2)中的数列![]()
![]()
![]() 满足不等式|
满足不等式|![]() -
-![]() |+|
|+|![]() -
-![]() |+┅+|
|+┅+|![]() -
-![]() |+|
|+|![]() -
-![]() |≤4,求
|≤4,求![]() 的值.
的值.
已知有穷数列{an}共有2k项(整数k≥2),首项a1=2,设该数列的前n项和为Sn,且an+1=(a-1)Sn+2(n=1,2,…,2k-1),其中常数a>1.
(1)求证:数列{an}是等比数列;
(2)若a=![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() log2(a1a2…an)(n=1,2,…,2k),求数列{bn}的通项公式;
log2(a1a2…an)(n=1,2,…,2k),求数列{bn}的通项公式;
(3)若(2)中的数列{bn}满足不等式.
|b1-![]() |+|b2-
|+|b2-![]() |+…+|b2k-1-
|+…+|b2k-1-![]() |+|b2k-
|+|b2k-![]() |≤4,求k的值.
|≤4,求k的值.
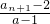 (n=1,2,3,…,2k-1),其中常数a>1.
(n=1,2,3,…,2k-1),其中常数a>1.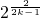 ,数列{bn}满足bn=
,数列{bn}满足bn=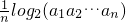 ,(n=1,2,3,…,2k),求证:1≤bn≤2;
,(n=1,2,3,…,2k),求证:1≤bn≤2; |+
|+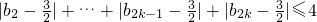 ,求k的最大值.
,求k的最大值. (n=1,2,3,…,2k-1),其中常数a>1.
(n=1,2,3,…,2k-1),其中常数a>1. ,数列{bn}满足bn=
,数列{bn}满足bn= ,(n=1,2,3,…,2k),求证:1≤bn≤2;
,(n=1,2,3,…,2k),求证:1≤bn≤2; |+
|+ ,求k的最大值.
,求k的最大值. (n=1,2,3,…,2k-1),其中常数a>1.
(n=1,2,3,…,2k-1),其中常数a>1. ,数列{bn}满足bn=
,数列{bn}满足bn= ,(n=1,2,3,…,2k),求证:1≤bn≤2;
,(n=1,2,3,…,2k),求证:1≤bn≤2; |+
|+ ,求k的最大值.
,求k的最大值.