摘要：18．解:(I)分别记“客人游览甲景点 .“客人游览乙景点 .“客人游览丙景点 为事件A1.A2.A3. 由已知A1.A2.A3相互独立.P(A1)=0.4.P(A2)=0.5. P(A3)=0.6. 客人游览的景点数的可能取值为0.1.2.3. 相应地.客人没有游览的景点数的可能取 值为3.2.1.0.所以的可能取值为1.3. P(=3)=P(A1·A2·A3)+ P() = P(A1)P(A2)P(A3)+P() =2×0.4×0.5×0.6=0.24. 1 3 P 0.76 0.24 P(=1)=1-0.24=0.76. 所以的分布列为 E=1×0.76+3×0.24=1.48. (Ⅱ)解法一 因为 所以函数上单调递增. 要使上单调递增.当且仅当 从而 解法二:的可能取值为1.3. 当=1时.函数上单调递增. 当=3时.函数上不单调递增.0 所以
网址：http://m.1010jiajiao.com/timu3_id_4469507[举报]
椭圆C的中心为坐标原点O，点A1，A2分别是椭圆的左、右顶点，B为椭圆的上顶点，一个焦点为F（
，0），离心率为
．点M是椭圆C上在第一象限内的一个动点，直线A1M与y轴交于点P，直线A2M与y轴交于点Q．
（I）求椭圆C的标准方程；
（II）若把直线MA1，MA2的斜率分别记作k1，k2，求证：k1k2=-
；
（III） 是否存在点M使|PB|=
|BQ|，若存在，求出点M的坐标，若不存在，说明理由．
查看习题详情和答案>>
| 3 |
| ||
| 2 |
（I）求椭圆C的标准方程；
（II）若把直线MA1，MA2的斜率分别记作k1，k2，求证：k1k2=-
| 1 |
| 4 |
（III） 是否存在点M使|PB|=
| 1 |
| 2 |
（2010•天津模拟）设O为坐标原点，点P的坐标（x-2，x-y）
（I）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（II）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率．
查看习题详情和答案>>
（I）在一个盒子中，放有标号为1，2，3的三张卡片，现从此盒中有放回地先后抽到两张卡片的标号分别记为x，y，求|OP|的最大值，并求事件“|OP|取到最大值”的概率；
（II）若利用计算机随机在[0，3]上先后取两个数分别记为x，y，求P点在第一象限的概率．
已知函数f（x）=x3-ax2-a2x．
（Ⅰ）若x=1时函数f（x）有极值，求a的值；
（Ⅱ）求函数f（x）的单调增区间；
（Ⅲ）若方程f（x）=0有三个不同的解，分别记为x1，x2，x3，证明：f（x）的导函数f′（x）的最小值为f′(
)．
查看习题详情和答案>>
（Ⅰ）若x=1时函数f（x）有极值，求a的值；
（Ⅱ）求函数f（x）的单调增区间；
（Ⅲ）若方程f（x）=0有三个不同的解，分别记为x1，x2，x3，证明：f（x）的导函数f′（x）的最小值为f′(
| x1+x2+x3 | 3 |
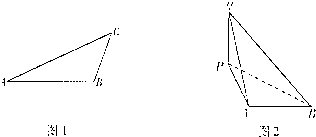某飞船返回仓顺利返回地球后，为了及时救出航天员，地面指挥中心在返回仓预计到达的区域内安排了三个救援中心（如图1分别记为A，B，C），B地在A地正东方向上，两地相距6km； C地在B地北偏东30°方向上，两地相距4km，假设P为航天员着陆点，某一时刻A救援中心接到从P点发出的求救信号，经过4s后，B、C两个救援中心也同时接收到这一信号，已知该信号的传播速度为1km/s．（I）求A、C两上救援中心的距离；
（II）求P相对A的方向角；
（III）试分析信号分别从P点处和P点的正上方Q点（如图2，返回仓经Q点垂直落至P点）处发出时，A、B两个救援中心收到信号的时间差的变化情况（变大还是变小），并证明你的结论． 查看习题详情和答案>>