题目内容
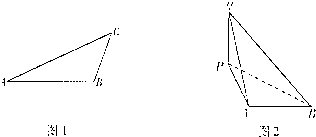 某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.
某飞船返回仓顺利返回地球后,为了及时救出航天员,地面指挥中心在返回仓预计到达的区域内安排了三个救援中心(如图1分别记为A,B,C),B地在A地正东方向上,两地相距6km; C地在B地北偏东30°方向上,两地相距4km,假设P为航天员着陆点,某一时刻A救援中心接到从P点发出的求救信号,经过4s后,B、C两个救援中心也同时接收到这一信号,已知该信号的传播速度为1km/s.(I)求A、C两上救援中心的距离;
(II)求P相对A的方向角;
(III)试分析信号分别从P点处和P点的正上方Q点(如图2,返回仓经Q点垂直落至P点)处发出时,A、B两个救援中心收到信号的时间差的变化情况(变大还是变小),并证明你的结论.
分析:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则可表示A,B,C的坐标,从而可求AC的距离;
(2)由题意,易判断P在以A,B为焦点的双曲线轭坐支上,从而可确定双曲线的方程,再与BC的垂直平分线的方程联立,可求P的坐标,从而问题得解.
(2)由题意,易判断P在以A,B为焦点的双曲线轭坐支上,从而可确定双曲线的方程,再与BC的垂直平分线的方程联立,可求P的坐标,从而问题得解.
解答:解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则A(-3,0),B(3,0),C(5,2
),∴AC=2
km,即A\C两个救援中心的距离为2
km
(2)∵PC=PB,∴P在BC线段的垂直平分线上;∵PB-PA=4,∴P在以A,B为焦点的双曲线轭坐支上,且AB=6,∴双曲线的方程为
-
=1(x<0),BC的垂直平分线的方程为x-
y-7=0,联立两方程解得x=-8,∴P(-8,5
),kPA=tan∠PAB=-
,∴∠PAB=120°,∴P在A点的北偏西300方向上.
| 3 |
| 19 |
| 19 |
(2)∵PC=PB,∴P在BC线段的垂直平分线上;∵PB-PA=4,∴P在以A,B为焦点的双曲线轭坐支上,且AB=6,∴双曲线的方程为
| x2 |
| 4 |
| y2 |
| 5 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查了解三角形的实际应用.解此类题的要点是建立适当的三角函数模型,利用三角函数的基本公式和定理进行求解.

练习册系列答案
相关题目


