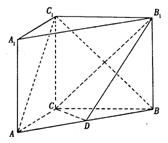
摘要:如图5所示..分别世.的直径.与两圆所在的平面均垂直..是的直径.,. (I)求二面角的大小, (II)求直线与所成的角.
网址:http://m.1010jiajiao.com/timu3_id_4468837[举报]
 (本题满分14分)如图,已知二次函数
(本题满分14分)如图,已知二次函数![]() ,直线l
,直线l![]() :x = 2,直线l
:x = 2,直线l![]() :y = 3tx(其中
:y = 3tx(其中![]() 1< t < 1,t为常数);若直线l
1< t < 1,t为常数);若直线l![]() 、l
、l![]() 与函数
与函数![]() 的图象所围成的封闭图形如图(5)阴影所示.(1)求y =
的图象所围成的封闭图形如图(5)阴影所示.(1)求y = ![]() ;(2)求阴影面积s关于t的函数s = u(t)的解析式;(3)若过点A(1,m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线,求实数m的取值范围.
;(2)求阴影面积s关于t的函数s = u(t)的解析式;(3)若过点A(1,m)(m≠4)可作曲线s=u(t)(t∈R)的三条切线,求实数m的取值范围.
 (本题14分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图)。
(本题14分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图)。![]()
![]()
(1)分别写出两种产品的收益与投资的函数关系;![]()
![]()
(2)该家庭现有20万元资金,全部用于理财投资,![]()
![]()
问:怎样分配资金能使投资获得最大收益,其最大
收益为多少万元?
查看习题详情和答案>>
 本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.
本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.(1)选修4-2:矩阵与变换
如图所示:△OAB在伸缩变换M作用下变为△OA1B1.
(i)求矩阵M的特征值及相应的特征向量;
(ii)求逆矩阵M-1以及(M-1)20
(2)选修4-4:坐标系与参数方程.
已知曲线C1的参数方程为
|
|
(i)若将曲线C1与C2上各点的横坐标都缩短为原来的一半,分别得到曲线C1和C2,求出曲线C1和C2的普通方程;
(ii)以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,求过极点且与C2垂直的直线的极坐标方程.
(3)选修4-5:不等式选讲
已知a,b,c为实数,且a+b+c+2-2m=0,a2+
| b 2 |
| 4 |
| c 2 |
| 9 |
(i)求证:a2+
| b 2 |
| 4 |
| c 2 |
| 9 |
| (a+b+c) 2 |
| 14 |
(ii)求实数m的取值范围. 查看习题详情和答案>>
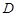 是
是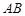 的中点。
的中点。 ;
;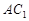 //平面
//平面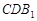 .
.