摘要：4．如图.已知椭圆.分别为椭圆的左.右焦点.A为椭圆的上顶点.直线交椭圆于另一点B． (Ⅰ)若.求椭圆的离心率, (Ⅱ)若椭圆的焦距为2.且.求椭圆的方程．
网址：http://m.1010jiajiao.com/timu3_id_4468437[举报]
如图，已知椭圆
，直线
的方程为
，过右焦点
的直线
与椭圆交于异于左顶点
的
两点，直线
，
交直线分别于点
，
．
（1）当
时，求此时直线的方程；
（2）试问，两点的纵坐标之积是否为定值？若是，求出该定值；若不是，请说明理由．
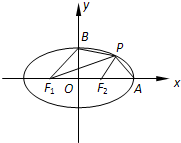如图，已知椭圆
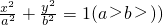，左、右焦点分别为F1，F2，右顶点为A，上顶点为B，P为椭圆上在第一象限内一点．
（1）若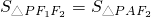
，求椭圆的离心率；
（2）若=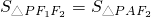
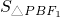，求直线PF1的斜率k；
（3）若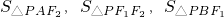
成等差数列，椭圆的离心率e
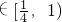，求直线PF1的斜率k的取值范围．
查看习题详情和答案>>
如图，已知椭圆
，左、右焦点分别为F1，F2，右顶点为A，上顶点为B，P为椭圆上在第一象限内一点，
（1）若
，求椭圆的离心率；
（2）若
，求直线PF1的斜率k；
（3）若
成等差数列，椭圆的离心率e∈
，求直线PF1的斜率k的取值范围。
，左、右焦点分别为F1，F2，右顶点为A，上顶点为B，P为椭圆上在第一象限内一点，（1）若
，求椭圆的离心率；（2）若
，求直线PF1的斜率k；（3）若
成等差数列，椭圆的离心率e∈，求直线PF1的斜率k的取值范围。 
，直线
的方程为
，过右焦点
的直线
与椭圆交于异于左顶点
的
两点，直线
、
交直线
、
．
时，求此时直线
，左、右焦点分别为F1，F2，右顶点为A，上顶点为B，P为椭圆上在第一象限内一点．
，求椭圆的离心率；
=
，求直线PF1的斜率k；
成等差数列，椭圆的离心率e
，求直线PF1的斜率k的取值范围．