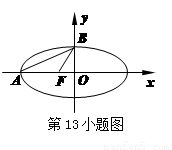题目内容
 如图,已知椭圆
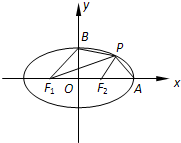
如图,已知椭圆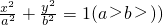 ,左、右焦点分别为F1,F2,右顶点为A,上顶点为B,P为椭圆上在第一象限内一点.
,左、右焦点分别为F1,F2,右顶点为A,上顶点为B,P为椭圆上在第一象限内一点.
(1)若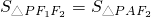 ,求椭圆的离心率;
,求椭圆的离心率;
(2)若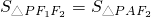 =
=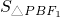 ,求直线PF1的斜率k;
,求直线PF1的斜率k;
(3)若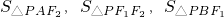 成等差数列,椭圆的离心率e
成等差数列,椭圆的离心率e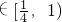 ,求直线PF1的斜率k的取值范围.
,求直线PF1的斜率k的取值范围.
解:(1)∵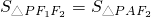 ∴F1F2=F2A
∴F1F2=F2A
∴a-c=2c
∴e=
(2)设直线PF1的方程为y=k(x+c),
∵
∴ PF1•
PF1• =
= PF1•
PF1•
∴b-kc=2kc
∴b=3kc
∵a=3c,a2-b2=c2
∴b=2 c
c
∴k=
(3)设 =t,则
=t,则 =
=
∵P在第一象限∴k>
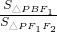 =
=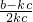
∴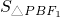 =
=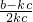 t
t
∴2t= +
+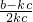 t
t
∴4kc=ak-ck+b-kc
∴k(6c-a)=b
∴k=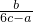
∴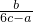 <
<
∴ <e<1
<e<1
又由已知e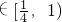 ,
,
∴e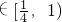 ,
,
∴k2= =
=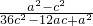
= =
=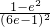 (令m=6e-1,∴e=
(令m=6e-1,∴e=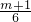 )
)
=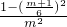 =
= ×
×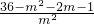
= ×(
×(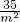 -
- -1)
-1)
∵e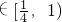 ,
,
∴ ≤m<5
≤m<5
∴ <
< ≤2∴0<k2≤
≤2∴0<k2≤
∴0<k≤
分析:(1)若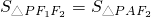 ,则F2为F1A的中点,从而得a、c间的等式,求得离心率;
,则F2为F1A的中点,从而得a、c间的等式,求得离心率;
(2)设直线PF1的方程为y=k(x+c),若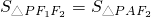 =
=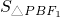 ,则点B、F2到直线PF1的距离相等,利用点到直线的距离公式即可得k、b、c间的关系,再由(1)即可求得斜率k的值
,则点B、F2到直线PF1的距离相等,利用点到直线的距离公式即可得k、b、c间的关系,再由(1)即可求得斜率k的值
(3)利用点到直线的距离公式,若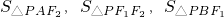 成等差数列,则k=
成等差数列,则k=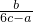 ,两边平方后,利用已知离心率范围,即可求得k的范围
,两边平方后,利用已知离心率范围,即可求得k的范围
点评:本题主要考查了椭圆的标准方程、椭圆的几何性质,椭圆的离心率的定义及其求法,直线与椭圆的位置关系,点到直线的距离公式的应用,有一定的运算量
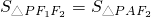 ∴F1F2=F2A
∴F1F2=F2A∴a-c=2c
∴e=

(2)设直线PF1的方程为y=k(x+c),
∵

∴
 PF1•
PF1• =
= PF1•
PF1•
∴b-kc=2kc
∴b=3kc
∵a=3c,a2-b2=c2
∴b=2
 c
c∴k=

(3)设
 =t,则
=t,则 =
=
∵P在第一象限∴k>

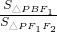 =
=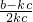
∴
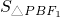 =
=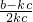 t
t∴2t=
 +
+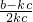 t
t∴4kc=ak-ck+b-kc
∴k(6c-a)=b
∴k=
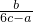
∴
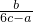 <
<
∴
 <e<1
<e<1又由已知e
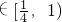 ,
,∴e
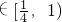 ,
,∴k2=
 =
=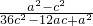
=
 =
=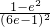 (令m=6e-1,∴e=
(令m=6e-1,∴e=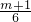 )
)=
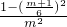 =
= ×
×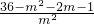
=
 ×(
×(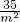 -
- -1)
-1)∵e
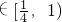 ,
,∴
 ≤m<5
≤m<5∴
 <
< ≤2∴0<k2≤
≤2∴0<k2≤
∴0<k≤

分析:(1)若
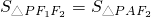 ,则F2为F1A的中点,从而得a、c间的等式,求得离心率;
,则F2为F1A的中点,从而得a、c间的等式,求得离心率;(2)设直线PF1的方程为y=k(x+c),若
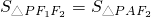 =
=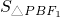 ,则点B、F2到直线PF1的距离相等,利用点到直线的距离公式即可得k、b、c间的关系,再由(1)即可求得斜率k的值
,则点B、F2到直线PF1的距离相等,利用点到直线的距离公式即可得k、b、c间的关系,再由(1)即可求得斜率k的值(3)利用点到直线的距离公式,若
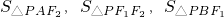 成等差数列,则k=
成等差数列,则k=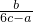 ,两边平方后,利用已知离心率范围,即可求得k的范围
,两边平方后,利用已知离心率范围,即可求得k的范围点评:本题主要考查了椭圆的标准方程、椭圆的几何性质,椭圆的离心率的定义及其求法,直线与椭圆的位置关系,点到直线的距离公式的应用,有一定的运算量

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 的左焦点为
的左焦点为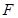 ,过点
,过点 两点,线段
两点,线段 的中点为
的中点为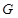 ,
, 轴和
轴和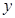 轴分别交于
轴分别交于 两点.
两点.
 ,求直线
,求直线 的面积为
的面积为 ,△
,△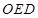 (
(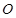 为原点)的面积为
为原点)的面积为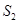 .试问:是否存在直线
.试问:是否存在直线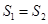 ?说明理由.
?说明理由.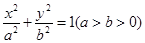 的左顶点为
的左顶点为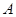 ,左焦点为
,左焦点为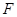 ,上顶点为
,上顶点为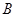 ,若
,若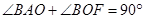 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .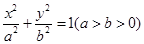 的左顶点为
的左顶点为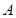 ,左焦点为
,左焦点为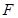 ,上顶点为
,上顶点为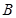 ,若
,若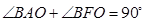 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.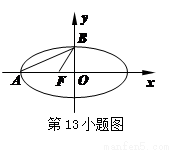
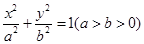 的左顶点为
的左顶点为 ,左焦点为
,左焦点为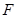 ,上顶点为
,上顶点为 ,若
,若 ,则该椭圆的离心率是
.
,则该椭圆的离心率是
.