摘要：作曲线的切线切点为Q1.设Q1点在x轴上的投影是点p1.又过点p1作曲线c的切线切点为Q2.设Q2在x轴上的投影是p2-.依此下去.得到一系列点Q1.Q2.-.Qn.-.设点Qn的横坐标为an (1)求证:, (2)求证:, (3)求证:(注:) 高三第三次质量检测 1-5 D A A C A 6-10 D D B C B 11-12 B C
网址：http://m.1010jiajiao.com/timu3_id_4466736[举报]
过点P(1，0)作曲线C：
的切线，切点为Q1，设Q1在
轴上的投影是Pl，又过P1作曲线C的切线，切点为Q2，设Q2在轴上的投影是P2，……依次下去，得到一系列Q1、Q2、…、Q
，设点Q横坐标为
．
(1)求
的值，并求出与
的关系；
(2)令
，设数列{
}的前
项和为
，求
.
已知函数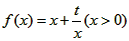
，过点P(1，0)作曲线y=f（x）的两条切线PM，PN，切点分别为M，N，
（1）当t=2时，求函数f(x)的单调递增区间；
（2）设|MN|=g（t），试求函数g（t）的表达式；
（3）在（2）的条件下，若对任意的正整数n，在区间[2，n+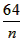
]内，总存在m+1个数a1，a2，....，am，
am+1，使得不等式g（a1）+g（a2）+...+g（am）<g（am+1）成立，求m的最大值
查看习题详情和答案>>
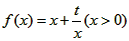，过点P(1，0)作曲线y=f（x）的两条切线PM，PN，切点分别为M，N，（1）当t=2时，求函数f(x)的单调递增区间；
（2）设|MN|=g（t），试求函数g（t）的表达式；
（3）在（2）的条件下，若对任意的正整数n，在区间[2，n+
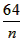]内，总存在m+1个数a1，a2，....，am，am+1，使得不等式g（a1）+g（a2）+...+g（am）<g（am+1）成立，求m的最大值
已知函数
，过点P(1，0)作曲线y＝f(x)的两条切线PM、PN，切点分别为M、N．
(1)当t＝2时，求函数f(x)的单调递增区间；
(2)设|MN|＝g(t)，试求函数g(t)的表达式
(3)在(2)的条件下，若对任意的正整数n，在区间[
]内总存在m＋1个实数a1，a2，…，am，am+1，使得不等式g(a1)＋g(a2)＋…＋g(am)＜g(am+1)成立，求m的最大值．
，过点P(1，0)作曲线y＝f(x)的两条切线PM，PN，切点分别为M，N．
内总存在m＋1个实数λ1，λ2……λm，λm+1使得不等式g(λ1)＋g(λ2)＋…＋g(λm)＜g(λm+1)成立，求m的最大值．