摘要：7．若a>b, f (x)在[b, a]上单调递减.则y=f -1(x)必满足( ). (A)在[b,a]上也是单调递减 (B)在[f (b), f (a)]上是单调递减 (C)在[f -1(a), f -1(b)]上是单调递减 (D)在[f (a), f (b)]上是单调递减
网址：http://m.1010jiajiao.com/timu3_id_4465224[举报]
（本题满分14分）已知二次函数
．
（1）若a>b>c， 且f（1）=0，证明f（x）的图象与x轴有2个交点；
（2）若 对
，方程
有2个不等实根，
；
（3）在（1）的条件下，是否存在m∈R，使f（m）=－ a成立时，f（m+3）为正数，若
存在，证明你的结论，若不存在，说明理由.
查看习题详情和答案>>
（本题满分14分）已知二次函数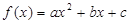
．
（1）若a>b>c， 且f（1）=0，证明f（x）的图象与x轴有2个交点；
（2）若 对
，方程
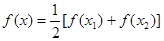有2个不等实根，
；
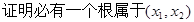（3）在（1）的条件下，是否存在m∈R，使f（m）=－ a成立时，f（m+3）为正数，若
存在，证明你的结论，若不存在，说明理由.
查看习题详情和答案>>
定义在区间（0，
）上的函f(x)满足：（1）f(x)不恒为零；（2）对任何实数x、q,都有
.
（1）求证：方程f(x)=0有且只有一个实根；
（2）若a>b>c>1,且a、b、c成等差数列，求证：
；
（3）（本小题只理科做）若f(x) 单调递增，且m>n>0时，有
，求证：
．
，方程
有2个不等实根，
．
>0.
)<f(x－
);