摘要：如果..是任意向量.则下列等式不一定成立的是---------------( ) (A) (+)+=+(+) (B) (+)·=·+· (C) m(+)=m+m (D) (·)·=(·)
网址：http://m.1010jiajiao.com/timu3_id_4461367[举报]
在平面直角坐标系xOy中，Ω是一个平面点集，如果存在非零平面向量
，对于任意P∈Ω，均有Q∈Ω，使得
=
+
，则称
为平面点集Ω的一个向量周期．现有以下四个命题：
①若平面点集Ω存在向量周期
，则k
（k∈Z，k≠0）也是Ω的向量周期；
②若平面点集Ω形成的平面图形的面积是一个非零常数，则Ω不存在向量周期；
③若平面点集Ω={（x，y）|x＞0，y＞0}，则
=（-1，2）为Ω的一个向量周期；
④若平面点集Ω={（x，y）|y=|sinx|-|cosx|}，则
=（
，0）为Ω的一个向量周期．
其中正确的命题个数是（ ）
| a |
| OQ |
| OP |
| a |
| a |
①若平面点集Ω存在向量周期
| a |
| a |
②若平面点集Ω形成的平面图形的面积是一个非零常数，则Ω不存在向量周期；
③若平面点集Ω={（x，y）|x＞0，y＞0}，则
| b |
④若平面点集Ω={（x，y）|y=|sinx|-|cosx|}，则
| c |
| π |
| 2 |
其中正确的命题个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
定义：对于映射f：A→B，如果A中的不同元素有不同的象，且B中的每一个元素都有原象，则称f：A→B为一一映射．如果存在对应关系φ，使A到B成为一一映射，则称A和B具有相同的势．给出下列命题：
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
，
}，其中
，
是不共线向量，B={
|
与
，
共面的任意向量}，则A和B不可能具有相同的势；
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为
查看习题详情和答案>>
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为
①③④
①③④
．下列命题：
①相等的向量，它们的坐标相等；反之，若数轴上两个向量的坐标相等，则这两个向量相等；
②对于任何一个实数，数轴上存在一个确定的点与之对应；
③数轴上向量
的坐标是一个数，实数的绝对值为线段AB的长度，如果起点指向终点的方向与数轴同方向，则这个实数取正数，反之取负数；
④起点和终点重合的向量是零向量，它的方向是任意的，它的坐标是0.
其中正确命题的个数是( )
A．1 B．2 C．3 D．4
查看习题详情和答案>>
，
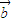}，其中
，
是不共线向量，B={
|
与
，
共面的任意向量}，则A和B不可能具有相同的势；
，
}，其中
|