摘要:18. 甲.乙两人进行乒乓球比赛.在每一局比赛中.甲获胜的概率为P. (I)如果甲.乙两人共比赛4局.甲恰好负2局的概率不大于其恰好胜3局的概率.试求P的取值范围. (Ⅱ)若.当采用3局2胜制的比赛规则时.求甲获胜的概率.- (Ⅲ)如果甲.乙两人比赛6局.那么甲恰好胜3局的概率可能是吗?为什么?
网址:http://m.1010jiajiao.com/timu3_id_4455072[举报]
(本小题满分12分)
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为![]() ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为![]() ,且各局胜负相互独立,比赛停止时一共已打ξ局.
,且各局胜负相互独立,比赛停止时一共已打ξ局.
(1)列出随机变量ξ的分布列;(2)求ξ的期望值Eξ.
查看习题详情和答案>> (本小题满分12分) 甲、乙、丙三人按下面的规则进行乒乓球比赛: 第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.
,且各局胜负相互独立.
求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数 的分别列与期望E
的分别列与期望E .
.
 ,且各局胜负相互独立.
,且各局胜负相互独立. 求:(I)打满3局比赛还未停止的概率;
(II)比赛停止时已打局数
 的分别列与期望E
的分别列与期望E .
.(本小题满分12分)
甲,乙两人进行乒乓球比赛,约定每局胜者得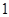 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多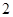 分或打满
分或打满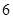 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为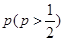 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为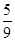 .
.
(1)求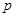 的值;
的值;
(2)设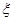 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量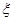 的分布列和数学期望
的分布列和数学期望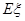 。
。
查看习题详情和答案>>
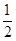 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: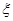 的分布列与期望
的分布列与期望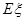 .
. 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 。
。