题目内容
(本小题满分12分)
甲,乙两人进行乒乓球比赛,约定每局胜者得 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为 .
.
(1)求 的值;
的值;
(2)设 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 。
。
(1) (2) 随机变量
(2) 随机变量 的分布列为:
的分布列为:



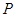




解析试题分析:(1)当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止,
故 ,解得
,解得 或
或 .
.
又 ,所以
,所以 . ……6分
. ……6分
(2)依题意知 的所有可能取值为2,4,6.
的所有可能取值为2,4,6. ,
, ,
, ,
,
所以随机变量 的分布列为:
的分布列为:
所以



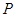



 的数学期望
的数学期望 . ……12分
. ……12分
考点:本小题主要考查相互独立事件同时发生的概率的计算和离散型随机变量的分布列和期望的计算,考查学生应用数学知识分析、解决实际问题的能力,难度一般.
点评:求离散型随机变量的分布列,首先要根据具体情况确定 的取值情况,然后利用排列、组合和概率知识求出
的取值情况,然后利用排列、组合和概率知识求出 取各个值的概率,求离散型随机变量的期望关键是写出离散型随机变量的分布列,然后利用公式计算.
取各个值的概率,求离散型随机变量的期望关键是写出离散型随机变量的分布列,然后利用公式计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对楼市“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25 | [25,35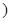 | [35,45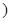 | [45,55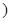 | [55,65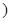 | [65,75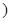 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 | 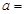 | 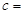 | |
| 不赞成 |  | 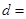 | |
| 合计 | | | |
 ,求随机变量
,求随机变量 的分布列及数学期望。
的分布列及数学期望。 在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为 (
( 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为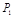 、
、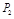 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
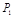 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
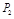 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.

 的数学期望
的数学期望 .
.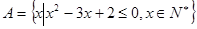 ,集合
,集合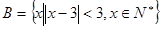 ,
,
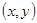 所有可能的结果;
所有可能的结果;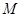 中任取一个元素,求“
中任取一个元素,求“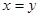 ”的概率
”的概率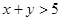 ”的概率.
”的概率.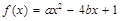 .
. 在区间
在区间 上是增函数的概率;
上是增函数的概率; 内的一点,求函数
内的一点,求函数