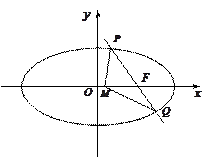摘要:21. 已知菱形的顶点在椭圆上.对角线所在直线的斜率为1. (Ⅰ)当直线过点时.求直线的方程, (Ⅱ)当时.求菱形面积的最大值. 请考生在第22.23.24题中任选一题做答.如果多做.则按所做的第一题记分.
网址:http://m.1010jiajiao.com/timu3_id_4454475[举报]
(本小题满分12分)
已知椭圆![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
求椭圆的方程;
设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,已知点
,已知点![]() 的坐标为(
的坐标为(![]() ),点
),点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值
的值
(本小题满分12分)
已知椭圆![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
求椭圆的方程;
设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,已知点
,已知点![]() 的坐标为(
的坐标为(![]() ),点
),点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值
的值
(本小题满分12分)
已知椭圆的中心在坐标原点 ,焦点在
,焦点在 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为 一个正方形的顶点.过右焦点
一个正方形的顶点.过右焦点 与
与 轴不垂直的直线
轴不垂直的直线 交椭圆于
交椭圆于 ,
, 两点.
两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在线段 上是否存在点
上是否存在点 ,使得以
,使得以 为邻边的平行四边形是菱形?
若存在,求出
为邻边的平行四边形是菱形?
若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.

查看习题详情和答案>>

 ,焦点在
,焦点在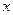 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为 一个正方形的顶点.过右焦点
一个正方形的顶点.过右焦点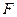 与
与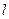 交椭圆于
交椭圆于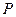 ,
,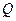 两点.
两点. 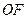 上是否存在点
上是否存在点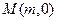 ,使得以
,使得以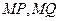 为邻边的平行四边形是菱形? 若存在,求出
为邻边的平行四边形是菱形? 若存在,求出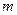 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.