一人造地球卫星绕地球做匀速圆周运动，假如该卫星变轨后仍做匀速圆周运动，动能减小为原来的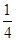，不考虑卫星质量的变化，则变轨前后卫星的(　　)

由上海飞往美国洛杉矶的飞机在飞越太平洋上空的过程中，如果保持飞机速度的大小和距离海面的高度均不变，则
A 飞机作的是匀速直线运动
B 飞机上的乘客对座椅的压力略大于地球对乘客的引力
C 飞机上的乘客对座椅的压力略小于地球对乘客的引力
D 飞机上的乘客对座椅的压力为零

已知万有引力恒量G，要计算地球的质量还必须已知某些数据，现给出以下各组数据。可以计算出地球质量的有

对于万有引力定律的数学表达式F＝，下列说法正确的是

用m表示地球通讯卫星（同步卫星）的质量，h表示它离地面的高度，R₀表示地球的半径，g₀表示地球表面处的重力加速度，ω₀表示地球自转的角速度.则通讯卫星所受的地球万有引力的大小为(　　)

A．等于mω02(R0+h)	B．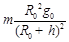
C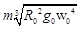．	D．以上结果都不正确

一星球半径和地球半径相同，它的表面重力加速度是地球表面重力加速度的2倍，则该星球质量是地球质量的（忽略地球、星球的自转）（   ）

甲、乙两个质点间的万有引力为F，若甲质点的质量不变，乙质点的质量增大为原来的2倍，同时它们间的距离减为原来的1/2，则甲、乙两个质点间的万有引力将变为（    ）

探测器绕月球做匀速圆周运动，变轨后在周期较小的轨道上仍做匀速圆周运动，则变轨后与变轨前相比(　　)

同步卫星A的运行速度为v1，向心加速度为a1，运转周期为T1；放在地球赤道上的物体B随地球自转的线速度为v2，向心加速度为a2，运转周期为T2；与赤道平面重合做匀速圆周 运动的近地卫星C的速度为v3，向心加速度为a3，运转周期为T3。比较上述各量的大小得（  ）

甲乙两个行星各有一个卫星绕其表面运行，已知甲乙两个卫星的周期之比为1：2，甲乙两个行星半径之比为2：1，则（  ）