题目内容
11.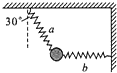 如图所示,两轻弹簧a、b悬挂一小球处于平衡状态,a弹簧与竖直方向成30°角,b弹
如图所示,两轻弹簧a、b悬挂一小球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b的劲度系数分别为k1、k2,则a、b的伸长量之比为( )
| A. | $\frac{{k}_{1}}{{k}_{2}}$ | B. | $\frac{{k}_{2}}{{k}_{1}}$ | C. | $\frac{2{k}_{2}}{{k}_{1}}$ | D. | $\frac{{k}_{2}}{2{k}_{1}}$ |
分析 对小球受力分析,受到重力和两个弹簧的弹力,根据平衡条件并运用合成法得到两个弹力之比,再结合胡克定律求解出伸长量之比.
解答 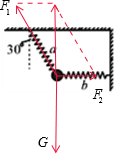 解:对小球受力分析,受到重力和两个弹簧的弹力,如图
解:对小球受力分析,受到重力和两个弹簧的弹力,如图
根据平衡条件,有:
$\frac{{F}_{2}}{{F}_{1}}=sin30°=\frac{1}{2}$
根据胡克定律,有:
F1=k1x1
F2=k2x2
解得:$\frac{{x}_{1}}{{x}_{2}}=\frac{2{k}_{2}}{{k}_{1}}$
故选:C
点评 本题考查共点力平衡条件的运用,关键是作图,三力中两个力的合力一定与第三个力等值、反向、共线.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
19. 在图中实线框所示的区域内同时存在着匀强磁场和匀强电场.一个质子恰好能沿直线MN从左至右通过这一区域.那么匀强磁场和匀强电场的方向可能为下列哪种情况( )
在图中实线框所示的区域内同时存在着匀强磁场和匀强电场.一个质子恰好能沿直线MN从左至右通过这一区域.那么匀强磁场和匀强电场的方向可能为下列哪种情况( )
 在图中实线框所示的区域内同时存在着匀强磁场和匀强电场.一个质子恰好能沿直线MN从左至右通过这一区域.那么匀强磁场和匀强电场的方向可能为下列哪种情况( )
在图中实线框所示的区域内同时存在着匀强磁场和匀强电场.一个质子恰好能沿直线MN从左至右通过这一区域.那么匀强磁场和匀强电场的方向可能为下列哪种情况( )| A. | 匀强磁场方向垂直于纸面向里,匀强电场方向竖直向上 | |
| B. | 匀强磁场方向竖直向上,匀强电场方向垂直于纸面向外 | |
| C. | 匀强磁场方向竖直向上,匀强电场方向垂直于纸面向里 | |
| D. | 匀强磁场和匀强电场的方向都水平向右 |
6.如图是某物体做直线运动的v-t图象,由图象可得到的正确结果是( )


| A. | t=1s时物体的加速度大小为1.5m/s2 | |
| B. | 物体3s内的平均速度大小为2.0m/s | |
| C. | 物体7s内的位移为12m | |
| D. | 物体第3s内位移6m |
3.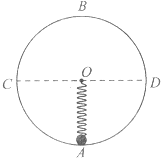 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为$k=\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为$k=\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
 如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为$k=\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )
如图所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球栓接,已知弹簧的劲度系数为$k=\frac{mg}{R}$,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v0,已知重力加速度为g,则( )| A. | 无论v0多大,小球均不会离开圆轨道 | |
| B. | 若在$\sqrt{2gR}<{v_0}<\sqrt{5gR}$则小球会在B、D间脱离圆轨道 | |
| C. | 只要${v}_{0}>2\sqrt{gR}$,小球就能做完整的圆周运动 | |
| D. | 只要小球能做完整圆周运动,则小球与轨道间最大压力与最小压力之差与v0无关 |
20.下列说法正确的是 ( )
| A. | 电荷放在电场中某点不受电场力,则该点的电势一定为零 | |
| B. | 电荷放在电场中某点不受电场力,则该点的电场强度一定为零 | |
| C. | 一小段通电导线放在磁场中某处不受磁场力,则该处的磁感应强度一定为零 | |
| D. | 一个闭合线圈放在磁场中某处穿过的磁通量为零,则该处的磁感应强度一定为零 |
1.下列措施是为了防止静电产生的危害?( )
| A. | 在高大的建筑物顶端装上避雷针 | B. | 静电复印 | ||
| C. | 在高大的烟囱中安装静电除尘器 | D. | 静电喷漆 |
 根据磁场会对载流导体产生作用力的原理,人们研究出一种新型的发射炮弹的装置--电磁炮,其原理简化为:水平放置的两个导轨相互平行,相距d=1m,处于竖直向上的匀强磁场中,一质量为m=2Kg的金属棒垂直于导轨上,与导轨间的动摩擦因数μ=0.1,当金属棒中的电流为I1=4A时,金属棒做匀速运动,取g=10m/s2.求:
根据磁场会对载流导体产生作用力的原理,人们研究出一种新型的发射炮弹的装置--电磁炮,其原理简化为:水平放置的两个导轨相互平行,相距d=1m,处于竖直向上的匀强磁场中,一质量为m=2Kg的金属棒垂直于导轨上,与导轨间的动摩擦因数μ=0.1,当金属棒中的电流为I1=4A时,金属棒做匀速运动,取g=10m/s2.求: 如图所示,在竖直平面内有一固定的光滑绝缘圆环,半径r=0.3m,圆环上套有一质量m=1×10-2kg、带电量q=+5xl0-5C的小球.匀强电场方向水平向右且与圆轨道所在平面平行.A为圆环最高点,B、C与圆心O在同一条水平线上.小球从A点静止释放,运动到B点时的速度vB=3m/s.重力加速度g取10m/s2.求:
如图所示,在竖直平面内有一固定的光滑绝缘圆环,半径r=0.3m,圆环上套有一质量m=1×10-2kg、带电量q=+5xl0-5C的小球.匀强电场方向水平向右且与圆轨道所在平面平行.A为圆环最高点,B、C与圆心O在同一条水平线上.小球从A点静止释放,运动到B点时的速度vB=3m/s.重力加速度g取10m/s2.求: