题目内容
3. 如图所示,半圆轨道竖直放置,半径R=0.4m,其底端与水平轨道相接,一个质量为m=0.2kg的滑块放在水平轨道C点上(轨道均为光滑).用一个水平的恒力作用于滑块,使滑块向右运动,当滑块到达半圆轨道的最低点A时撤去F,滑块能恰好通过圆的最高点B沿水平方向飞出,恰好落回到C点,则:
如图所示,半圆轨道竖直放置,半径R=0.4m,其底端与水平轨道相接,一个质量为m=0.2kg的滑块放在水平轨道C点上(轨道均为光滑).用一个水平的恒力作用于滑块,使滑块向右运动,当滑块到达半圆轨道的最低点A时撤去F,滑块能恰好通过圆的最高点B沿水平方向飞出,恰好落回到C点,则:(1)C离A多远?
(2)所需水平恒力多大?(取g=10m/s2).
分析 (1)由牛顿第二定律可以求出滑块到达B点的速度,滑块离开B后做平抛运动,应用平抛运动规律可以求出C与A间的距离.
(2)应用动能定理可以求出水平拉力大小.
解答 解:(1)滑块恰好通过最高点B,重力提供向心力,
在B点,由牛顿第二定律得:mg=m$\frac{{v}^{2}}{R}$,
代入数据解得:v=2m/s,
离开B后滑块做平抛运动,
水平方向:x=vt,
竖直方向:2R=$\frac{1}{2}$gt2,
代入数据解得:x=0.8m;
(2)从C到B过程中,由动能定理得:
Fx-mg•2R=$\frac{1}{2}$mv2-0,
代入数据解得:F=2.5N;
答:(1)C与A相距0.8m.
(2)所需水平恒力为2.5N.
点评 本题考查了求距离、拉力大小问题,分析清楚滑块的运动过程,应用牛顿第二定律、动能定理与平抛运动规律可以解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列说法正确的是( )
| A. | 没有外力作用,物体不会运动,这是牛顿第一定律的体现 | |
| B. | 力的国际单位制单位“牛顿”是根据牛顿第二定律定义的 | |
| C. | 一对作用力与反作用力总是大小相等,性质相同 | |
| D. | 物体的速度越大,其惯性也越大 |
16.由于某种原因,人造地球卫星的轨道半径减小了,那么,卫星的( )
| A. | 速率变小,周期变大 | B. | 速率变大,周期变大 | ||
| C. | 速率变大,周期变小 | D. | 速率变小,周期变小 |
13.如图甲,质量相等的a、b两物体,从斜面上的同一位置A由静止下滑,经B点在水平面上滑行一段时间后停下.不计经过B点时的能量损失,用传感器采集到它们的速度一时间图象如图图乙,则下列说法正确的是( )


| A. | a在水平面上滑行的距离比b的长 | |
| B. | a与斜面间的动摩擦因数比b的大 | |
| C. | 在整个运动过程中a,b两物体滑行的距离可能相等 | |
| D. | a在整个运动过程中克服摩擦力做的功比b的多 |
20. 如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )
如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )
 如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )
如图为“嫦娥一号”卫星撞月的模拟图,卫星从控制点开始沿撞月轨道在撞击点成功撞月,假设卫星绕月球做圆周运动的轨道半径为R,周期为T,引力常量为G,根据以上信息,可以求出( )| A. | 月球的质量 | B. | 地球的质量 | ||
| C. | “嫦娥一号”卫星的质量 | D. | 月球对“嫦娥一号”卫星的引力 |
15.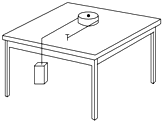 质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )
 质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上.一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌子边缘之间的摩擦都忽略不计,则重物下落过程中,工件的加速度为( )| A. | $\frac{mg}{2M}$ | B. | $\frac{mg}{M+m}$ | C. | $\frac{2mg}{M+4m}$ | D. | $\frac{2mg}{M+2m}$ |
13. 如图所示,圆形线圈垂直放在匀强磁场里,第1秒内磁场方向指向纸里,如图(乙).若磁感应强度大小随时间变化的关系如图(甲),那么,下面关于线圈中感应电流的说法正确的是( )
如图所示,圆形线圈垂直放在匀强磁场里,第1秒内磁场方向指向纸里,如图(乙).若磁感应强度大小随时间变化的关系如图(甲),那么,下面关于线圈中感应电流的说法正确的是( )
 如图所示,圆形线圈垂直放在匀强磁场里,第1秒内磁场方向指向纸里,如图(乙).若磁感应强度大小随时间变化的关系如图(甲),那么,下面关于线圈中感应电流的说法正确的是( )
如图所示,圆形线圈垂直放在匀强磁场里,第1秒内磁场方向指向纸里,如图(乙).若磁感应强度大小随时间变化的关系如图(甲),那么,下面关于线圈中感应电流的说法正确的是( )| A. | 在第1秒内感应电流增大,电流方向为逆时针 | |
| B. | 在第2秒内感应电流大小不变,电流方向为顺时针 | |
| C. | 在第3秒内感应电流大小不变,电流方向为逆时针 | |
| D. | 在第4秒内感应电流大小不变,电流方向为逆时针 |