题目内容
5.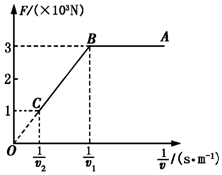 一辆汽车质量为2×103kg,额定功率为3×104W.在水平路面由静止开始作直线运动,运动中汽车所受阻力恒定,发动机的最大牵引力为3×103N,汽车以额定功率行驶100s时速度达到最大,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示,求:
一辆汽车质量为2×103kg,额定功率为3×104W.在水平路面由静止开始作直线运动,运动中汽车所受阻力恒定,发动机的最大牵引力为3×103N,汽车以额定功率行驶100s时速度达到最大,其行驶过程中牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示,求:(1)汽车能达到最大速度
(2)汽车由启动到最大速度时的位移.
分析 (1)根据图示得到最大速度时的牵引力,即可根据功率P=Fv求得最大速度;
(2)首先根据最大速度时的牵引力求得摩擦力,然后根据最大牵引力求得匀加速运动阶段的加速度,再由图得到匀加速运动的末速度即可求得匀加速运动的位移;然后根据动能定理求得额定功率启动阶段的位移.
解答 解:(1)由图可知,牵引力取得最小值F1=1000N时,汽车的速度最大为v2,又有汽车的额定功率为:P=3×104W,所以有:${v}_{2}=\frac{P}{{F}_{1}}=30m/s$;
(2)由(1)可知,当牵引力取得最小值F1=1000N时,汽车做匀速直线运动,速度达到最大值,故汽车受到的摩擦力为:f=F1=1000N;
汽车从静止开始以最大牵引力做匀加速直线运动,加速度为:$a=\frac{{F}_{AB}-f}{m}=1m/{s}^{2}$;
当汽车速度达到:${v}_{1}=\frac{P}{{F}_{AB}}=10m/s$后,汽车做恒定功率启动;
所以,汽车匀加速启动的位移为:${x}_{1}=\frac{{{v}_{1}}^{2}}{2a}=50m$;
汽车以额定功率启动时,只有摩擦力和牵引力做功,故由动能定理可得:$Pt-f{x}_{2}=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$;
所以,${x}_{2}=\frac{Pt-\frac{1}{2}m{{v}_{2}}^{2}+\frac{1}{2}m{{v}_{1}}^{2}}{f}$=$\frac{3×1{0}^{4}×100-\frac{1}{2}×2×1{0}^{3}×3{0}^{2}+\frac{1}{2}×2×1{0}^{3}×1{0}^{2}}{1000}=2200m$;
所以,汽车由启动到最大速度时的位移为x1+x2=2250m;
答:(1)汽车能达到最大速度为30m/s;
(2)汽车由启动到最大速度时的位移为2200m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

| A. | 原子中心有一个很小的原子核 | B. | 原子核是由质子和中子组成的 | ||
| C. | 原子质量几乎全部集中在原子核内 | D. | 原子的正电荷全部集中在原子核内 |
 如图所示,一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s.下列说法正确的是( )
如图所示,一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s.下列说法正确的是( )| A. | 球棒对垒球的平均作用力大小为360N | |
| B. | 球棒对垒球的平均作用力大小为1260N | |
| C. | 球棒对垒球做的功为36J | |
| D. | 球棒对垒球做的功为126J |
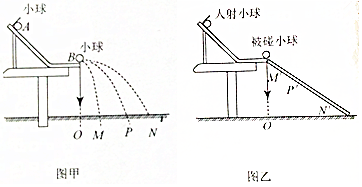
 如图所示,绝缘细杆倾斜固定放置,小球M套在杆上课沿杆滑动,M通过绝缘轻质弹簧与固定的小球N相连,杆和弹簧处于同一竖直面内,现使M、N带电荷量不同的异种电荷,将M从位置A由静止释放,M运动到B点时弹簧与杆垂直且为原长,运动到C点时速度减为零,M在A、C两点时弹簧长度相同,下列说法正确的是( )
如图所示,绝缘细杆倾斜固定放置,小球M套在杆上课沿杆滑动,M通过绝缘轻质弹簧与固定的小球N相连,杆和弹簧处于同一竖直面内,现使M、N带电荷量不同的异种电荷,将M从位置A由静止释放,M运动到B点时弹簧与杆垂直且为原长,运动到C点时速度减为零,M在A、C两点时弹簧长度相同,下列说法正确的是( )| A. | M从A点滑到C点的过程,M和弹簧组成的系统的机械能守恒 | |
| B. | M从A点滑到C点的过程中,M的重力势能减少量等于其克服摩擦力做的功 | |
| C. | M从A点滑到B点的过程中,弹簧的弹力做正功,电场力做负功 | |
| D. | M在A、C两点的电势能相等 |
 圆环轨道固定在竖直平面内,由于圆环存在摩擦,一个可视为质点的小 球,在圆环内至少可以做20次完整的圆周运动,当它第20次经过环的最低点时速度大小为1m/s,第18次经过环的最低点时的速度大小为 5m/s,则小球笫16次经过环的最低点时的速度v的大小一定满足( )
圆环轨道固定在竖直平面内,由于圆环存在摩擦,一个可视为质点的小 球,在圆环内至少可以做20次完整的圆周运动,当它第20次经过环的最低点时速度大小为1m/s,第18次经过环的最低点时的速度大小为 5m/s,则小球笫16次经过环的最低点时的速度v的大小一定满足( )| A. | 大于 7 m/s | B. | 等于 7 m/s | C. | 大于 9m/s | D. | 等于 9 m/s |
 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )| A. | 卫星运行的角速度为$\frac{π}{2t}$ | B. | 地球的质量为$\frac{gR}{G}$ | ||
| C. | 卫星运行的线速度为$\frac{πR}{2t}$ | D. | 卫星距地面的高度($\frac{4{{gR}^{2}t}^{2}}{{π}^{2}}$) |
 两个等量异种电荷的连线的垂直平分线上有a、b、c三点,如图所示,下列说法正确的是( )
两个等量异种电荷的连线的垂直平分线上有a、b、c三点,如图所示,下列说法正确的是( )| A. | a、b两点的场强相同 | |
| B. | 电荷从a点移到b点静电力不做功 | |
| C. | a、b、c三点的电势都大于无穷远处的电势 | |
| D. | 两个等量异种电荷的连线上c点场强最强 |