题目内容
17. 如图所示,A是容积很大的玻璃容器,B是内径很小的玻璃管,B的左端与A相通,右端开口,B中有一段水银柱将一定质量的空气封闭在A中,当把A放在冰水混合物中时,B的左管比右管中水银高30cm;当B的左管比右管的水银面低30cm时,A中气体的温度是多少?(设大气压强p0=76mHg)
如图所示,A是容积很大的玻璃容器,B是内径很小的玻璃管,B的左端与A相通,右端开口,B中有一段水银柱将一定质量的空气封闭在A中,当把A放在冰水混合物中时,B的左管比右管中水银高30cm;当B的左管比右管的水银面低30cm时,A中气体的温度是多少?(设大气压强p0=76mHg)
分析 由于A的体积很大而B管很细,所以A容器的体积可认为不变,列出初末状态的参量,根据查理定律列式求解;
解答 解:由于A的体积很大而B管很细,所以A容器的体积可认为不变.以A中体为研究对象:
初始状态温度T1=273K,
压强p1=p0-h=46cmHg,
末状态压强p2=p0+h=106cmHg,
由查理定律得$\frac{{p}_{1}^{\;}}{{T}_{1}^{\;}}=\frac{{p}_{2}^{\;}}{{T}_{2}^{\;}}$,
T2=$\frac{{p}_{2}^{\;}}{{p}_{1}^{\;}}{T}_{1}^{\;}=\frac{106}{46}×273K=629K$
答:A中气体的温度是629K
点评 本题考查气体实验定律的综合应用,关键是确定气体的状态参量,判断气体发生的是什么变化过程,在选择合适的实验定律求解.

练习册系列答案
相关题目
18.关于速度、加速度、合外力的关系,下列说法正确的是( )
| A. | 合外力不等于零时,物体的加速度和速度也一定都不等于零 | |
| B. | 合外力变小时,物体运动的速度可能变大 | |
| C. | 物体做加速直线运动时,合外力的方向一定与速度方向相同 | |
| D. | 加速度的方向与合外力的方向总是一致的,但与速度的方向有可能相反 |
8. 如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端的距离为L.当传送带分别以v1、v2的速度逆时针转动时(v1<v2),绳中的拉力分别为F1、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为t1、t2,达到左端速度分别为v′1,v′2,则下列说法可能正确的是( )
如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端的距离为L.当传送带分别以v1、v2的速度逆时针转动时(v1<v2),绳中的拉力分别为F1、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为t1、t2,达到左端速度分别为v′1,v′2,则下列说法可能正确的是( )
 如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端的距离为L.当传送带分别以v1、v2的速度逆时针转动时(v1<v2),绳中的拉力分别为F1、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为t1、t2,达到左端速度分别为v′1,v′2,则下列说法可能正确的是( )
如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端的距离为L.当传送带分别以v1、v2的速度逆时针转动时(v1<v2),绳中的拉力分别为F1、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为t1、t2,达到左端速度分别为v′1,v′2,则下列说法可能正确的是( )| A. | F1=F2 | B. | F1<F2 | C. | v′1=v′2 | D. | t1>t2 |
5. 如图所示,水平转台上有一个质量为m=2kg的物块,用长为L=0.1m的细绳将物块连接在转轴上,细丝与竖直转轴的夹角为θ=53°角,此时绳中张力为零,物块与转台间最大静摩擦力等于重力的0.2倍,物块随转台由静止开始缓慢加速转动,g=10m/s2,sin53°=0.8,cos53°=0.6,则:( )
如图所示,水平转台上有一个质量为m=2kg的物块,用长为L=0.1m的细绳将物块连接在转轴上,细丝与竖直转轴的夹角为θ=53°角,此时绳中张力为零,物块与转台间最大静摩擦力等于重力的0.2倍,物块随转台由静止开始缓慢加速转动,g=10m/s2,sin53°=0.8,cos53°=0.6,则:( )
 如图所示,水平转台上有一个质量为m=2kg的物块,用长为L=0.1m的细绳将物块连接在转轴上,细丝与竖直转轴的夹角为θ=53°角,此时绳中张力为零,物块与转台间最大静摩擦力等于重力的0.2倍,物块随转台由静止开始缓慢加速转动,g=10m/s2,sin53°=0.8,cos53°=0.6,则:( )
如图所示,水平转台上有一个质量为m=2kg的物块,用长为L=0.1m的细绳将物块连接在转轴上,细丝与竖直转轴的夹角为θ=53°角,此时绳中张力为零,物块与转台间最大静摩擦力等于重力的0.2倍,物块随转台由静止开始缓慢加速转动,g=10m/s2,sin53°=0.8,cos53°=0.6,则:( )| A. | 至绳中刚好出现拉力时,转台对物块做的功为0.16J | |
| B. | 至绳中刚好出现拉力时,转台对物块做的功为0.24J | |
| C. | 至转台对物块支持力刚好为零时,转台对物块做的功为$\frac{8}{15}$J | |
| D. | 至转台对物块支持力刚好为零时,转台对物块做的功为$\frac{16}{15}$J |
2. 如图所示.轻质导体棒ab两个端点分别搭接在两个竖直放置、电阻不计、半径相等的金属圆环上,圆环通过电刷与导线c、d相接.c、d两个端点接在匝数比n1:n2=l0:1的理想变压器原线圈两端,变压器副线圈接一滑动变阻器R0,匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为L(电阻不计),绕与ab平行的水平轴(也是两圆环的中心轴)OO′以角速度ω匀速转动.如果滑动变阻器的阻值为R时,通过电流表的电流为I,则( )
如图所示.轻质导体棒ab两个端点分别搭接在两个竖直放置、电阻不计、半径相等的金属圆环上,圆环通过电刷与导线c、d相接.c、d两个端点接在匝数比n1:n2=l0:1的理想变压器原线圈两端,变压器副线圈接一滑动变阻器R0,匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为L(电阻不计),绕与ab平行的水平轴(也是两圆环的中心轴)OO′以角速度ω匀速转动.如果滑动变阻器的阻值为R时,通过电流表的电流为I,则( )
 如图所示.轻质导体棒ab两个端点分别搭接在两个竖直放置、电阻不计、半径相等的金属圆环上,圆环通过电刷与导线c、d相接.c、d两个端点接在匝数比n1:n2=l0:1的理想变压器原线圈两端,变压器副线圈接一滑动变阻器R0,匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为L(电阻不计),绕与ab平行的水平轴(也是两圆环的中心轴)OO′以角速度ω匀速转动.如果滑动变阻器的阻值为R时,通过电流表的电流为I,则( )
如图所示.轻质导体棒ab两个端点分别搭接在两个竖直放置、电阻不计、半径相等的金属圆环上,圆环通过电刷与导线c、d相接.c、d两个端点接在匝数比n1:n2=l0:1的理想变压器原线圈两端,变压器副线圈接一滑动变阻器R0,匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为L(电阻不计),绕与ab平行的水平轴(也是两圆环的中心轴)OO′以角速度ω匀速转动.如果滑动变阻器的阻值为R时,通过电流表的电流为I,则( )| A. | 滑动变阻器上消耗的功率为P=100I2R | |
| B. | 变压器原线圈两端的电压U1=10IR | |
| C. | ab沿环转动过程中受到的最大安培力F=$\sqrt{2}$BIL | |
| D. | 取ab在环的最低端时t=0,则导体棒ab中感应电流的表达式是i=$\sqrt{2}$Isinω |
6. 如图所示,虚线a、b、c代表电场中的三个等差等势面,ab的间距大于bc的间距.实线为一带电的粒子仅在电场力作用下通过该区域时的运动轨迹,P、M为轨迹上的两个点,由此可知( )
如图所示,虚线a、b、c代表电场中的三个等差等势面,ab的间距大于bc的间距.实线为一带电的粒子仅在电场力作用下通过该区域时的运动轨迹,P、M为轨迹上的两个点,由此可知( )
 如图所示,虚线a、b、c代表电场中的三个等差等势面,ab的间距大于bc的间距.实线为一带电的粒子仅在电场力作用下通过该区域时的运动轨迹,P、M为轨迹上的两个点,由此可知( )
如图所示,虚线a、b、c代表电场中的三个等差等势面,ab的间距大于bc的间距.实线为一带电的粒子仅在电场力作用下通过该区域时的运动轨迹,P、M为轨迹上的两个点,由此可知( )| A. | 粒子在M点受到的电场力比在P点受到的电场力小 | |
| B. | 粒子在P、M两点间的运动过程,电场力可能做正功 | |
| C. | 粒子在M点的电势能一定比在P点的电势能大 | |
| D. | 三个等势面中,a的电势一定最高 |
7.将一质量为m的小球从空中O点以速度v0水平抛出,飞行一段时间后,小球经过P点时动能为Ek,不计空气阻力,关于小球从O点到P点过程说法正确的是( )
| A. | 速度变化量大小为$\sqrt{\frac{2{E}_{k}}{m}}$-v0 | |
| B. | 小球的高度下降$\frac{{E}_{k}}{mg}$-$\frac{{{v}_{0}}^{2}}{2g}$ | |
| C. | 小球运动的平均速度为$\frac{{v}_{0}}{2}$+$\sqrt{\frac{{E}_{k}}{2m}}$ | |
| D. | 小球重力的平均功率为$\frac{mg}{2}$$\sqrt{\frac{2{E}_{k}}{m}-{{v}_{0}}^{2}}$ |
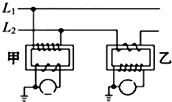 如图,L1和L2是输电线,若已知电压互感器变压比为1000:1,电流互感器变流比为100:1,并且知道电压表示数为220V,电流表示数为10A,则图中甲为电压互感器(填“甲”或“乙”),且输电线的输送功率为2.2×109 w.
如图,L1和L2是输电线,若已知电压互感器变压比为1000:1,电流互感器变流比为100:1,并且知道电压表示数为220V,电流表示数为10A,则图中甲为电压互感器(填“甲”或“乙”),且输电线的输送功率为2.2×109 w. 如图所示,一定质量的理想气体从状态A经等压过程到状态B,此过程中气体压强p=1.0×105Pa,吸收的热量Q=7.0×102J,求
如图所示,一定质量的理想气体从状态A经等压过程到状态B,此过程中气体压强p=1.0×105Pa,吸收的热量Q=7.0×102J,求