题目内容
12. 如图,水平细杆上套一质量为0.54kg的小环A,用轻绳将质量为0.5kg的小球B与A相连.B受到始终与水平成53°角的风力作用,与A一起向右匀速运动,此时轻绳与水平方向夹角为37°,运动过程中B球始终在水平细杆的下方,求:(取g=10m/s2,sin37°=0.6,cos37°=0.8)
如图,水平细杆上套一质量为0.54kg的小环A,用轻绳将质量为0.5kg的小球B与A相连.B受到始终与水平成53°角的风力作用,与A一起向右匀速运动,此时轻绳与水平方向夹角为37°,运动过程中B球始终在水平细杆的下方,求:(取g=10m/s2,sin37°=0.6,cos37°=0.8)(1)B对绳子的拉力;
(2)A与杆间的动摩擦因数.
分析 (1)由B受力平衡得到绳子对B的拉力,再根据牛顿第三定律得到B对绳子的拉力;
(2)根据A的受力平衡得到A受到的支持力和摩擦力,进而得到动摩擦因数.
解答 解:(1)小球B向右匀速运动,那么小球受力平衡,所以,绳子拉力T=mBgsin37°=0.5×10×0.6N=3N;
那么,由牛顿第三定律可知:B对绳子的拉力为3N;
(2)对A进行受力分析可知:摩擦力f=Tcos37°=2.4N,A对杆的正压力FN=mAg+Tsin37°=0.54×10+3×0.6(N)=7.2N;
所以,A与杆间的动摩擦因数$μ=\frac{f}{{F}_{N}}$=$\frac{1}{3}$;
答:(1)B对绳子的拉力为3N;
(2)A与杆间的动摩擦因数为$\frac{1}{3}$.
点评 求解物体受力大小,一般根据物体运动状态得到加速度,然后由牛顿第二定律求得合外力,再根据物体受力分析求得外力.

练习册系列答案
相关题目
2.某人用绳提着质量为m的物体,使物体以加速度a(a<g)沿竖直方向加速下降高度h;稍停后,此人再用绳提着该物体以加速度a沿竖直方向加速提升高度h.这两个过程中人对物体做的总功为( )
| A. | 2mah | B. | 0 | C. | 2mgh | D. | m(g+a)h |
3.关于理想气体的内能,下列说法正确的是( )
| A. | 气体在膨胀时,内能可能不变 | |
| B. | 质量和温度都相同的气体,内能一定相同 | |
| C. | 一定质量的某种理想气体在等压压缩过程中,内能一定减少 | |
| D. | 气体温度不变,整体运动速度越大,其内能越大 |
20. 如图所示是欧姆表的工作原理图,若电流表G的满偏电流为1g=500μA,干电池的电动势为1.5V,
如图所示是欧姆表的工作原理图,若电流表G的满偏电流为1g=500μA,干电池的电动势为1.5V,
(1)这只欧姆表的总内阻为3kΩ.
(2)把电流表G的电流刻度值对应的欧姆表表盘电阻填在下表中:
 如图所示是欧姆表的工作原理图,若电流表G的满偏电流为1g=500μA,干电池的电动势为1.5V,
如图所示是欧姆表的工作原理图,若电流表G的满偏电流为1g=500μA,干电池的电动势为1.5V,(1)这只欧姆表的总内阻为3kΩ.
(2)把电流表G的电流刻度值对应的欧姆表表盘电阻填在下表中:
| 电流刻度 | 0 | 100μA | 250μA | 300μA | 500μA |
| 电阻刻度 |
7.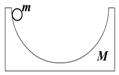 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
 如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的$\frac{1}{2}$光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )| A. | m能到达圆弧轨道右侧的最高位置与初始位置等高 | |
| B. | m能到达圆弧轨道右侧的最高位置比初始位置低,不会滑出圆弧轨道 | |
| C. | m能到达圆弧轨道右侧的最高位置比初始位置高,将滑出圆弧轨道 | |
| D. | m到达圆弧轨道右侧最高位置时,M将会向左移动一段位移 |
17. 如图所示,质量分别为MA、MB的两小球A、B,且MA>MB,A、B穿过一绕过一定滑轮的轻绳,绳子末端与地面的距离相同,两小球在同一高度.小球A、B与轻绳的滑动摩擦力都为重力的K倍(0<K<1),设最大静摩擦力等于滑动摩擦力.现由静止同时释放A、B两个小球,不计定滑轮的质量,忽略绳子与定滑轮之间的摩擦力,不计空气阻力,则下列说法正确的是( )
如图所示,质量分别为MA、MB的两小球A、B,且MA>MB,A、B穿过一绕过一定滑轮的轻绳,绳子末端与地面的距离相同,两小球在同一高度.小球A、B与轻绳的滑动摩擦力都为重力的K倍(0<K<1),设最大静摩擦力等于滑动摩擦力.现由静止同时释放A、B两个小球,不计定滑轮的质量,忽略绳子与定滑轮之间的摩擦力,不计空气阻力,则下列说法正确的是( )
 如图所示,质量分别为MA、MB的两小球A、B,且MA>MB,A、B穿过一绕过一定滑轮的轻绳,绳子末端与地面的距离相同,两小球在同一高度.小球A、B与轻绳的滑动摩擦力都为重力的K倍(0<K<1),设最大静摩擦力等于滑动摩擦力.现由静止同时释放A、B两个小球,不计定滑轮的质量,忽略绳子与定滑轮之间的摩擦力,不计空气阻力,则下列说法正确的是( )
如图所示,质量分别为MA、MB的两小球A、B,且MA>MB,A、B穿过一绕过一定滑轮的轻绳,绳子末端与地面的距离相同,两小球在同一高度.小球A、B与轻绳的滑动摩擦力都为重力的K倍(0<K<1),设最大静摩擦力等于滑动摩擦力.现由静止同时释放A、B两个小球,不计定滑轮的质量,忽略绳子与定滑轮之间的摩擦力,不计空气阻力,则下列说法正确的是( )| A. | A对绳的作用力与B对绳的作用力的大小相同 | |
| B. | A、B、绳、滑轮组成的系统机械能守恒 | |
| C. | 刚释放时aA>aB | |
| D. | 刚释放时aA=aB |
4. 质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
 质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )| A. | A球的速度最大时,角BOA的角平分线在竖直方向 | |
| B. | A球的速度最大时,两小球的重力势能之和最小 | |
| C. | A球的速度最大时,A球在其运动圆周的最低点 | |
| D. | A球的速度最大时,两直角边与竖直方向的夹角为45° |
5. 月球自转周期T与它绕地球做匀速圆周运动的公转周期相同,假如“嫦娥四号”卫星在近月轨道(轨道半径近似为月球半径)做匀速圆周运动的周期为T0,如图所示,PQ为月球直径,某时刻Q点离地面O最近,且P、Q、O共线,月球表面的重力加速度为g0,万有引力常量为G,则( )
月球自转周期T与它绕地球做匀速圆周运动的公转周期相同,假如“嫦娥四号”卫星在近月轨道(轨道半径近似为月球半径)做匀速圆周运动的周期为T0,如图所示,PQ为月球直径,某时刻Q点离地面O最近,且P、Q、O共线,月球表面的重力加速度为g0,万有引力常量为G,则( )
 月球自转周期T与它绕地球做匀速圆周运动的公转周期相同,假如“嫦娥四号”卫星在近月轨道(轨道半径近似为月球半径)做匀速圆周运动的周期为T0,如图所示,PQ为月球直径,某时刻Q点离地面O最近,且P、Q、O共线,月球表面的重力加速度为g0,万有引力常量为G,则( )
月球自转周期T与它绕地球做匀速圆周运动的公转周期相同,假如“嫦娥四号”卫星在近月轨道(轨道半径近似为月球半径)做匀速圆周运动的周期为T0,如图所示,PQ为月球直径,某时刻Q点离地面O最近,且P、Q、O共线,月球表面的重力加速度为g0,万有引力常量为G,则( )| A. | 月球的密度为ρ=$\frac{3π}{{G{T^2}}}$ | |
| B. | 月球的第一宇宙速度$v=\frac{{{g_0}{T_0}}}{2π}$ | |
| C. | 从图示位置开始计时经过$\frac{T}{2}$,P点离地心O是最近的 | |
| D. | 要使“嫦娥四号”卫星在月球的背面P点着陆,需提前加速 |
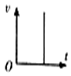
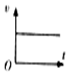
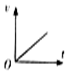
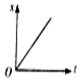 如图是物运动的x-t图象,则选项中与之相对应的v-t图象是( )
如图是物运动的x-t图象,则选项中与之相对应的v-t图象是( )