题目内容
一颗人造卫星靠近某行星表面做匀速圆周运动,经过时间t,卫星运行的路程为s,运动半径转过的角度为1rad,引力常量设为G,求:(1)卫星运行的周期;
(2)该行星的质量.
【答案】分析:知道描述圆周运动快慢的物理量的含义.
研究人造卫星绕行星表面做匀速圆周运动,根据万有引力提供向心力列出等式,求出中心体的质量.
解答:解:(1)根据角速度的定义式得:
ω=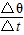 =
= rad/s
rad/s
根据线速度的定义式得:
v=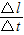 =
=
根据周期与角速度的关系得:
T=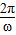 =2πt
=2πt
根据线速度和角速度的关系得:R=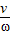 =s
=s
(2)研究人造卫星绕行星表面做匀速圆周运动,根据万有引力提供向心力列出等式:
 =m
=m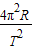 得出:M=
得出:M=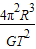 =
=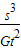
答:(1)卫星运行的周期是2πt
(2)该行星的质量是 .
.
点评:要清楚线速度、角速度、周期的定义和物理量之间的关系.
通过万有引力提供向心力求出中心体的质量.
研究人造卫星绕行星表面做匀速圆周运动,根据万有引力提供向心力列出等式,求出中心体的质量.
解答:解:(1)根据角速度的定义式得:
ω=
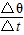 =
= rad/s
rad/s根据线速度的定义式得:
v=
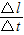 =
=
根据周期与角速度的关系得:
T=
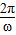 =2πt
=2πt根据线速度和角速度的关系得:R=
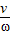 =s
=s(2)研究人造卫星绕行星表面做匀速圆周运动,根据万有引力提供向心力列出等式:
 =m
=m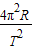 得出:M=
得出:M=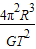 =
=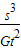
答:(1)卫星运行的周期是2πt
(2)该行星的质量是
 .
.点评:要清楚线速度、角速度、周期的定义和物理量之间的关系.
通过万有引力提供向心力求出中心体的质量.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目