题目内容
16.2007年10月24日18时5分,我国在西昌卫星发射中心用“长征三号甲”运载火箭将“嫦娥一号”卫星成功送入太空.“嫦娥一号”绕月探测飞行将完成四大科学探测任务获取月球全表现三维图象;分析月球表面化学元素和物质类型的含量和分布;探测月壤特性;探测4万至40万公里间地月空间环境.现已知地球自转周期为T0,月球半径R,卫星距离月球高度h,月球表面重力加速度为g,万有引力常量G.下列说法中正确的是( )| A. | “嫦娥一号”卫星绕月球运行的速率v=$\sqrt{g(R+h)}$ | |
| B. | “嫦娥一号”卫星和地球的角速度之比为$\frac{{T}_{0}}{2π}$$\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}$ | |
| C. | 利用以上数据可以求出月球的质量 | |
| D. | 月球的密度ρ=$\frac{3Gg}{4πR}$ |
分析 由题意可知,可以求出卫星的轨道半径,卫星绕月球做匀速圆周运动,由月球的万有引力提供向心力,根据牛顿第二定律求出“嫦娥一号”的线速度与角速度;然后结合密度公式分析能否求出月球的质量和密度.根据月球对卫星的万有引力等于卫星的重力,得到月球表面的重力加速度.
解答 解:设该卫星的运行周期为T、质量为m,月球的半径为R、质量为M,卫星距月球表面的高度为h,由题意知,卫星的轨道半径r=R+h,
“嫦娥一号”卫星在月球表面受到的吸引力:mg=$\frac{GMm}{{R}^{2}}$,所以,g=$\frac{GM}{{R}^{2}}$
A、卫星绕月球做圆周运动,万有引力提供向心力,
由牛顿第二定律得:G$\frac{Mm}{(R+h)^{2}}$=m$\frac{{v}^{2}}{R+h}$
所以:v=$\sqrt{\frac{g{R}^{2}}{R+h}}$.故A错误;
B、卫星绕月球做圆周运动,万有引力提供向心力,
由牛顿第二定律得:G$\frac{Mm}{(R+h)^{2}}$=mω2(R+h)
所以:ω=$\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}$
地球自转的角速度:$ω′=\frac{2π}{{T}_{0}}$
所以“嫦娥一号”卫星和地球的角速度之比为$\frac{{T}_{0}}{2π}$$\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}$.故B正确;
C、卫星绕月球做圆周运动,万有引力提供向心力,
由牛顿第二定律得:G$\frac{Mm}{(R+h)^{2}}$=m$(\frac{2π}{T})^{2}$(R+h),
则月球质量M=$\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}$,故C正确;
D、月球的密度ρ=$\frac{M}{V}$=$\frac{\frac{4{π}^{2}(R+h)^{3}}{G{T}^{2}}}{\frac{4}{3}π{R}^{3}}$=$\frac{3π(R+h)^{3}}{G{T}^{2}{R}^{3}}$,故D错误;
故选:BC
点评 已知卫星的运行周期和轨道半径,可求出月球的质量,这个结果可推广到行星绕太阳:若已知行星的公转半径和周期,可求出太阳的质量.


(1)按电路原理图甲连接实物电路图乙
(2)连好电路后,该同学开始实验,闭合电键S后,他发现电流表的示数不为零,电压表的示数不为零,他用多用电表的电压挡检查电路,把两表笔分别接a、b和b、c及d、e时,示数均为零,把两表笔接c、d时,其示数与电压表示数相同,检查各接线柱均未接错,且接触良好,各接线之间也未发生短路,由此可推断故障原因应是滑动变阻器断路.
(3)排除故障后,该同学顺利完成实验,测得下列五组数据:
| U(V) | 1.20 | 1.00 | 0.80 | 0.60 |
| I(A) | 0.10 | 0.17 | 0.23 | 0.30 |
(4)考虑电表本身电阻对测量结果的影响,造成本实验系统误差的原因:伏特表内阻的分流作用造成系统误差..
(5)实验所得的电池电动势E和内电阻r的测量值与真实值相比较E测<E真,r测<r真(填<、=或>).
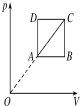
| A. | 由状态A变化到状态B,气体分子的平均动能增大 | |
| B. | 由状态A变化到状态C,气体内能不变 | |
| C. | 由A经B到C的过程与由A经D到C的过程,气体对外做功相同 | |
| D. | 由A经B到C、由A经D到C、由A直接到C的三个过程中,气体均吸热,但是吸热量不同 |
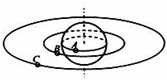 中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高时间分辨率对地观测卫星.如图所示,A是静止在赤道上随地球自转的物体;B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列关系正确的是( )
中国航天局在2015年年底发射了高分四号卫星,这是中国首颗地球同步轨道高时间分辨率对地观测卫星.如图所示,A是静止在赤道上随地球自转的物体;B、C是同在赤道平面内的两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是高分四号卫星.则下列关系正确的是( )| A. | 物体A随地球自转的角速度大于卫星B的角速度 | |
| B. | 卫星B的线速度小于卫星C的线速度 | |
| C. | 物体A随地球自转的向心加速度小于卫星C的向心加速度 | |
| D. | 物体A随地球自转的周期大于卫星C的周期 |
| A. | 做平抛运动的物体相等时间内速度增量是变大 | |
| B. | 平抛运动是匀变速曲线运动 | |
| C. | 圆周运动中的合力就是向心力 | |
| D. | 匀速圆周运动是速度不变的运动 |
| A. | an=$\frac{{v}^{2}}{r}$ | B. | T=2πr | C. | ω=$\sqrt{\frac{{a}_{n}}{r}}$ | D. | v=ωr |
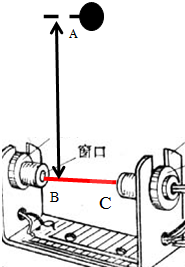 某兴趣小组利用光电门数字计时器测当地的重力加速度,实验装置如图所示,(实验器材有,光电门数字计时器、刻度尺、小钢球、电源)BC为光电门激光器发出的水平激光线,一半径为R的小球从A点由静止释放,改变小球释放位置,发现小球挡住光的时间为均不相同.
某兴趣小组利用光电门数字计时器测当地的重力加速度,实验装置如图所示,(实验器材有,光电门数字计时器、刻度尺、小钢球、电源)BC为光电门激光器发出的水平激光线,一半径为R的小球从A点由静止释放,改变小球释放位置,发现小球挡住光的时间为均不相同.