题目内容
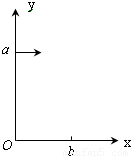 如图所示,在x>0,y>0的空间存在沿y轴负方向的匀强电场,场强大小为E.一粒子源不断地发射相同的带电粒子,粒子的初速度恒定,并从y轴上的a处沿x轴正方向射入匀强电场中,粒子经电场作用后恰好从x轴上的b处射出.已知oa=2ob=L.若撤去电场,在此区域加一方向垂直于xoy平面的匀强磁场,磁感强度大小为B,其它条件不变,粒子仍恰好从b处射出,不计粒子的重力和粒子之间的相互作用.
如图所示,在x>0,y>0的空间存在沿y轴负方向的匀强电场,场强大小为E.一粒子源不断地发射相同的带电粒子,粒子的初速度恒定,并从y轴上的a处沿x轴正方向射入匀强电场中,粒子经电场作用后恰好从x轴上的b处射出.已知oa=2ob=L.若撤去电场,在此区域加一方向垂直于xoy平面的匀强磁场,磁感强度大小为B,其它条件不变,粒子仍恰好从b处射出,不计粒子的重力和粒子之间的相互作用.(1)求带电粒子的比荷(q/m).
(2)带电粒子在电场中的运动时间t1与带电粒子在磁场中的运动时间t2之比是多大?(sin53°=0.8,cos53°=0.6)
【答案】分析:带电粒子在电场中做类平抛运动,由平抛运动的规律可列出x、y方向的位移、电场强度、带电粒子的比荷及粒子的初速度的表达式,从而可求出带电粒子的比荷.当带电粒子在磁场时,做匀速圆周运动.根据进出两点可确定圆周运动的圆心,从而可画出运动轨迹,得出已知长度L与圆周半径间的关系.最后可算出带电粒子在电场中运动时间与在磁场中运动时间的比值.
解答:解:(1)设粒子的初速度为v,空间存在电场时,粒子进入电场后做类平抛运动,
设粒子在场区运动的时间为t1,沿x方向上: (1)
(1)
沿y方向上有:L=
 (2)
(2)
联立(1)(2))可解得有:8mv2=qEL (3)
若改加磁场,粒子进入磁场后做匀速圆周运动,
设圆周半径为R,由几何关系知:

(L-R)2+( )2=R2,
)2=R2,
解得R= (4)
(4)
又因洛仑兹力提供向心力,所以有Bqv0= (5)
(5)
由(4)(5)联立可解得:8 mv=5qBL (6)
由(3)(6)两式消去v得:
故带电粒子的比荷是
(2)带电粒子在磁场中的圆轨迹如上图所示
圆心到原点的距离
而b到原点o的距离
因此b 到圆心直线与y轴的夹角为53°
所以圆弧对应的圆心角为θ=127°
则根据周期公式,粒子在磁场中的运动时间为:
t2= ?
? =
=
代入:t1= 和
和 =
= ,
,
可得: =
= ≈0.36
≈0.36
点评:本题考查带电粒子在电场中做类平抛运动处理的规律:在x方向位移与时间关系;在y方向位移与时间关系,然后消去时间找到y与x方向的位移间关系.掌握在磁场中做匀速圆周运动处理的方法:定圆心、画圆弧、求半径.
解答:解:(1)设粒子的初速度为v,空间存在电场时,粒子进入电场后做类平抛运动,
设粒子在场区运动的时间为t1,沿x方向上:
 (1)
(1)沿y方向上有:L=

 (2)
(2)联立(1)(2))可解得有:8mv2=qEL (3)
若改加磁场,粒子进入磁场后做匀速圆周运动,
设圆周半径为R,由几何关系知:

(L-R)2+(
 )2=R2,
)2=R2,解得R=
 (4)
(4)又因洛仑兹力提供向心力,所以有Bqv0=
 (5)
(5)由(4)(5)联立可解得:8 mv=5qBL (6)
由(3)(6)两式消去v得:

故带电粒子的比荷是

(2)带电粒子在磁场中的圆轨迹如上图所示
圆心到原点的距离

而b到原点o的距离

因此b 到圆心直线与y轴的夹角为53°
所以圆弧对应的圆心角为θ=127°
则根据周期公式,粒子在磁场中的运动时间为:
t2=
 ?
? =
=
代入:t1=
 和
和 =
= ,
,可得:
 =
= ≈0.36
≈0.36点评:本题考查带电粒子在电场中做类平抛运动处理的规律:在x方向位移与时间关系;在y方向位移与时间关系,然后消去时间找到y与x方向的位移间关系.掌握在磁场中做匀速圆周运动处理的方法:定圆心、画圆弧、求半径.

练习册系列答案
相关题目
 如图所示,在x>0、y>0(第Ⅰ象限)的空间存在沿y轴负方向的匀强电场,场强大小为E,一个粒子源发射相同的带正电粒子,粒子的初速度恒定,并从y轴上的P(0,2L)点沿x轴正方向射入匀强电场中,粒子经电场作用后恰好从x轴上的Q(L,0)点射出.若撤去电场,在此区域加一方向垂直于xoy平面的匀强磁场,磁感强度大小为B,其它条件不变,粒子仍恰好从Q射出,不计粒子的重力和粒子之间的相互作用,(取:
如图所示,在x>0、y>0(第Ⅰ象限)的空间存在沿y轴负方向的匀强电场,场强大小为E,一个粒子源发射相同的带正电粒子,粒子的初速度恒定,并从y轴上的P(0,2L)点沿x轴正方向射入匀强电场中,粒子经电场作用后恰好从x轴上的Q(L,0)点射出.若撤去电场,在此区域加一方向垂直于xoy平面的匀强磁场,磁感强度大小为B,其它条件不变,粒子仍恰好从Q射出,不计粒子的重力和粒子之间的相互作用,(取: 如图所示,在x>0,y>0的空间中有一匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场.不计重力的影响,则下列有关说法中正确的是( )
如图所示,在x>0,y>0的空间中有一匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电量为q的带正电粒子,从在x轴上的某点P沿着与x轴成30°角的方向射入磁场.不计重力的影响,则下列有关说法中正确的是( ) 如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电量为q的带电粒子,在x轴上到原点的距离为x0的P点,以平行于y轴的初速度射入磁场.在磁场作用下沿垂直于y轴的方向射出磁场.不计重力的影响,由这些信息可以确定的是( )
如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电量为q的带电粒子,在x轴上到原点的距离为x0的P点,以平行于y轴的初速度射入磁场.在磁场作用下沿垂直于y轴的方向射出磁场.不计重力的影响,由这些信息可以确定的是( ) 如图所示,在x<0且y<0的区域内存在垂直纸面向里的匀强磁场,磁感应强度大小为B,在x>0且y<0的区域内存在沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场,结果带电粒子从y轴的N点射出磁场而进入匀强电场,经电场偏转后打到x轴上的P点,已知
如图所示,在x<0且y<0的区域内存在垂直纸面向里的匀强磁场,磁感应强度大小为B,在x>0且y<0的区域内存在沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场,结果带电粒子从y轴的N点射出磁场而进入匀强电场,经电场偏转后打到x轴上的P点,已知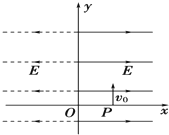 如图所示,在x>0的空间内存在沿x轴正方向的匀强电场,电场强度为E;在x<0的空间内存在沿x轴负方向的匀强电场,场强大小也等于E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:
如图所示,在x>0的空间内存在沿x轴正方向的匀强电场,电场强度为E;在x<0的空间内存在沿x轴负方向的匀强电场,场强大小也等于E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求: