题目内容
如图，半径为R的
圆弧支架竖直放置，支架底AB离地的距离为2R，圆弧边缘C处有一小定滑轮，一轻绳两端系着质量分别为m1与m2的物体，挂在定滑轮两边，且m1＞m2，开始时m1、m2均静止，m1、m2可视为质点，不计一切摩擦．求：（1）m1释放后经过圆弧最低点A时的速度
（2）若m1到最低点时绳突然断开，求m1落地点离A点水平距离．
【答案】分析：（1）设m1运动到圆弧最低点时速度为v1，此时m2的速度为v2，根据几何关系求出两速度的关系，由m1与m2组成系统，机械能守恒，根据机械能守恒定律列式即可求解；
（2）断绳后m1做平抛运动，根据平抛运动的基本规律即可求解．
解答：解：（1）设m1运动到圆弧最低点时速度为v1，此时m2的速度为v2，则：v2=v1sin45° …①
由m1与m2组成系统，机械能守恒，有：
…②
由①②两式可得：
（2）断绳后m1做平抛运动
…③
s=v1t…④
由③④两式可得：s=4R
答：（1）m1释放后经过圆弧最低点A时的速度为
；
（2）若m1到最低点时绳突然断开，m1落地点离A点水平距离为4R
．
点评：本题主要考查了机械能守恒定律及平抛运动基本规律的应用，能根据几何关系求解m1运动到圆弧最低点时速度与此时m2的速度的关系，难度适中．
（2）断绳后m1做平抛运动，根据平抛运动的基本规律即可求解．
解答：解：（1）设m1运动到圆弧最低点时速度为v1，此时m2的速度为v2，则：v2=v1sin45° …①
由m1与m2组成系统，机械能守恒，有：
…②由①②两式可得：
（2）断绳后m1做平抛运动
…③s=v1t…④
由③④两式可得：s=4R
答：（1）m1释放后经过圆弧最低点A时的速度为
；（2）若m1到最低点时绳突然断开，m1落地点离A点水平距离为4R
．点评：本题主要考查了机械能守恒定律及平抛运动基本规律的应用，能根据几何关系求解m1运动到圆弧最低点时速度与此时m2的速度的关系，难度适中．
练习册系列答案
相关题目
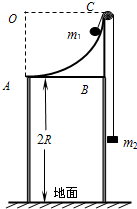如图，半径为R的1/4圆弧支架竖直放置，支架底AB离地的距离为2R，圆弧边缘C处有一小定滑轮，一轻绳两端系着质量分别为m1与m2的物体，挂在定滑轮两边，且m1＞m2，开始时m1、m2均静止，m1、m2可视为质点，不计一切摩擦．求：
如图，半径为 r的绝缘光滑环固定在竖直平面内，环上套有一质量为 m，带电量为+q的珠子，现欲加一个与圆环面平行的匀强电场，使珠子由最高点A从静止开始释放，沿圆弧经过B、C刚好能运动到D，
圆弧支架竖直放置，支架底AB离地的距离为2R，圆弧边缘C处有一小定滑轮，一轻绳两端系着质量分别为m1与m2的物体，挂在定滑轮两边，且m1＞m2，开始时m1、m2均静止，m1、m2可视为质点，不计一切摩擦。求：