Question

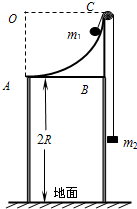如图，半径为R的1/4圆弧支架竖直放置，支架底AB离地的距离为2R，圆弧边缘C处有一小定滑轮，一轻绳两端系着质量分别为m₁与m₂的物体，挂在定滑轮两边，且m₁＞m₂，开始时m₁、m₂均静止，m₁、m₂可视为质点，不计一切摩擦．求：
（1）m₁释放后经过圆弧最低点A时的速度；
（2）若m₁到最低点时绳突然断开，求m₁落地点离A点水平距离；
（3）为使m₁能到达A点，m₁与m₂之间必须满足什么关系？

Answer 1

分析：（1）两个滑块构成的系统只有重力势能和动能相互转化，机械能守恒；同时绳子不可伸长，沿着绳子方向的分速度相等；
（2）绳子断开后，m₁落地落地前做平抛运动，根据平抛运动的分位移公式列式求解；
（3）为使m₁能到达A点，则要求其速度大于零即可．

解答：解：（1）设m₁运动到最低点时速度为v₁，此时m₂的速度为v₂，速度分解如图，

沿着绳子方向的速度相等，得：v₂=v₁sin45°  
由m₁与m₂组成系统，机械能守恒，有m1gR-m 2g

2

R=

1

2

m1

υ

2 1

+

1

2

m2

υ

2 2

   
由上述两式求得υ1=2

(m1- 2 m2)gR 2m1+m2

（2）断绳后m₁做平抛运动
t1=

2h g

=2

R g

s=v₁t₁
两式联立解得s=4R
（3）m₁能到达A点满足条件v₁≥0 
又υ1=2

(m1- 2 m2)gR 2m 1+m2

解得：m1≥

2

m2
答：（1）m₁释放后经过圆弧最低点A时的速度为2

(m1- 2 m2)gR 2m1+m2

；
（2）若m₁到最低点时绳突然断开，m₁落地点离A点水平距离为4R；
（3）为使m₁能到达A点，m₁与m₂之间必须满足关系为m1≥

2

m2．

点评：本题关键是单个物体机械能不守恒，但两个物体系统机械能守恒；同时要明确通过绳子、轻杆连接的物体，沿着绳子、杆子方向的分速度一定相等．