题目内容
13. 如图所示,12个相同的木块放在水平地面上排成一条直线,相邻两木块接触但不粘连,每个木块的质量m=1.2kg,长度l=0.5m.木块原来都静止,它们与地面间的动摩擦因数均为μ1=0.1,在左边第一个木块的左端放一质量M=1kg的小铅块(可视为质点),它与各木块间的动摩擦因数为μ2=0.5,现突然给铅块一个向右的初速度v0=9m/s,使其在木块上滑行.设木块与地面间及铅块与木块间的最大静摩擦力均等于滑动糜擦力,重力加速度g=10m/s2.求:
如图所示,12个相同的木块放在水平地面上排成一条直线,相邻两木块接触但不粘连,每个木块的质量m=1.2kg,长度l=0.5m.木块原来都静止,它们与地面间的动摩擦因数均为μ1=0.1,在左边第一个木块的左端放一质量M=1kg的小铅块(可视为质点),它与各木块间的动摩擦因数为μ2=0.5,现突然给铅块一个向右的初速度v0=9m/s,使其在木块上滑行.设木块与地面间及铅块与木块间的最大静摩擦力均等于滑动糜擦力,重力加速度g=10m/s2.求:(1)小铅块相对木块滑动时小铅块的加速度大小;
(2)铅块下面的木块刚发生运动时铅块的瞬时速度大小.
分析 (1)通过对木块的受力分析知,铅块对木块的滑动摩擦力水平向右,地面给木块的静摩擦力水平向左,由牛顿第二定律即可求出铅块的加速度;
(2)当铅块对木板的摩擦力大于地面对木块的摩擦力时,木块开始运动;根据动能定理求铅块的瞬时速度.
解答 解:(1)设定水平向右为正向.对铅块:f木铅=μ2Mg=0.5×1×10=5 N
所以铅块的加速度:$a=\frac{{f}_{木铅}}{M}=\frac{5}{1}=5m/{s}^{2}$
(2)对下方n个物块刚滑动,应当满足的条件是:${f_{铅木}}>μ_1^{\;}(nmg+Mg)$
又:f铅木=f木铅
则木块开始滑动:$n<\frac{{f}_{铅木}-{μ}_{1}Mg}{{μ}_{1}mg}=\frac{10}{3}$
即当铅块滑至倒数第三块木块上时,木块开始滑动.
设铅块滑上倒数第三块木块时的初速度为v1,则对于铅块连续滑过前9木块的过程中:$-{f}_{木铅}•9L=\frac{1}{2}M{v}_{1}^{2}-\frac{1}{2}M{v}_{0}^{2}$
解得:v1=6m/s
v1也是铅块刚滑到倒数第三块木块这一瞬间铅块对木块的相对速度,在此瞬间木块静止.
答:(1)小铅块相对木块滑动时小铅块的加速度大小是5m/s2;
(2)铅块下面的木块刚发生运动时铅块的瞬时速度大小是6m/s.
点评 本题是相对运动的题目,关键要对每个物体分别分析其运动情况,判断木块能否运动,利用运动学的基本公式,再根据速度和位移的关系及牛顿第二定律求解.

练习册系列答案
相关题目
4. 如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a、b、c是轮边缘上的三个质点,则偏心轮转动过程中a、b、c三个质点( )
如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a、b、c是轮边缘上的三个质点,则偏心轮转动过程中a、b、c三个质点( )
 如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a、b、c是轮边缘上的三个质点,则偏心轮转动过程中a、b、c三个质点( )
如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a、b、c是轮边缘上的三个质点,则偏心轮转动过程中a、b、c三个质点( )| A. | 角速度ωa>ωb>ωc | B. | 线速度va=vb=vc | ||
| C. | 向心加速度aa<ab<ac | D. | 向心力Fa<Fb<Fc |
1.两个紧密接触的粗糙物体,发生相对滑动时,两者间的一对滑动摩擦力做功之和( )
| A. | 一定为负 | B. | 一定为零 | C. | 可能为正 | D. | 可能为零 |
1. 图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )
图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )
 图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )
图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )| A. | 副线圈两端的电压比为4:1 | B. | 原线圈输入电流比为1:2 | ||
| C. | 副线圈的接入匝数比为2:1 | D. | 原线圈输入功率比为2:1 |
8.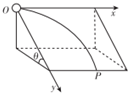 质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )
质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )
 质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )
质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )| A. | t1>t2>t3 | B. | x1>x2>x3 | ||
| C. | 落地时质点的速度与x轴夹角相同 | D. | 落地时质点重力的功率相同 |
5.以下说法正确的是( )
| A. | 电荷处于磁场中不一定受到洛伦兹力 | |
| B. | 电荷在磁场中一定受到洛伦兹力 | |
| C. | 某运动电荷在某处未受到洛伦兹力,该处的磁感成强度一定为零 | |
| D. | 洛伦兹力不能改变运动电荷的速度 |
 如图所示,是某物体的v-t图象.在前20秒内,物体位移的大小是125m,物体改变运动方向的时刻是15s末,在最后5秒内,物体做匀加速直线运动.
如图所示,是某物体的v-t图象.在前20秒内,物体位移的大小是125m,物体改变运动方向的时刻是15s末,在最后5秒内,物体做匀加速直线运动. 如图所示,ABC直角三棱镜,顶角A为30°,BC边水平且长度为L,一束光线竖直向下从AB的中点O射入棱镜,折射光线刚好从C点射出,光在真空中的速度为c,求:
如图所示,ABC直角三棱镜,顶角A为30°,BC边水平且长度为L,一束光线竖直向下从AB的中点O射入棱镜,折射光线刚好从C点射出,光在真空中的速度为c,求: 如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内做圆周运动,小球在最高点的速度用v表示.当v由零逐渐增大,向心力F增大(填“增大”“减小”或“不变”);当v由$\sqrt{gL}$逐渐减小时,杆对小球的弹力F0增大(填“增大”“减小”或“不变”).
如图所示,长为L的轻杆,一端固定一个小球,另一端固定在光滑的水平轴上,使小球在竖直平面内做圆周运动,小球在最高点的速度用v表示.当v由零逐渐增大,向心力F增大(填“增大”“减小”或“不变”);当v由$\sqrt{gL}$逐渐减小时,杆对小球的弹力F0增大(填“增大”“减小”或“不变”).