题目内容
8. 一个绕中心线AB以一定的角速度转动的圆环,P、Q为环上两点,位置如图所示,下列说法正确的是( )
一个绕中心线AB以一定的角速度转动的圆环,P、Q为环上两点,位置如图所示,下列说法正确的是( )| A. | P、Q两点的角速度相等 | B. | P、Q两点的线速度相等 | ||
| C. | P、Q两点的角速度之比为$\sqrt{3}$:1 | D. | P、Q两点的线速度之比为1:1 |
分析 共轴转动的点,角速度大小相等,由几何知识求出P、Q转动的半径之比,结合v=rω求出线速度之比.
解答 解:AC、P、Q两点共轴转动,角速度大小相等.故A正确,C错误.
BD、设圆环的半径为R,根据几何知识可得:P、Q转动的半径分别为:
rP=Rsin60°
rQ=Rsin30°
P、Q两点角速度相等,根据v=rω知,P、Q两点的线速度之比为:vP:vQ=rP:rQ=Rsin60°:Rsin30°=$\sqrt{3}$:1.故BD错误.
故选:A
点评 解决本题的关键知道共轴转动的点角速度大小相等,知道线速度与角速度的关系式v=rω,并能灵活运用.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19. 如图所示,虚线a、b、c代表电场中的三个等势面,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q为质点先后通过电场时轨迹上的两个点,由此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q为质点先后通过电场时轨迹上的两个点,由此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q为质点先后通过电场时轨迹上的两个点,由此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q为质点先后通过电场时轨迹上的两个点,由此可知( )| A. | 三个等势面中,a的电势最高 | B. | 质点在Q点时,加速度较小 | ||
| C. | 质点通过P点时动能较大 | D. | 质点通过Q时电势能较小 |
16.关于匀速圆周运动的向心加速度的说法,正确的是( )
| A. | 向心加速度恒定不变 | |
| B. | 由a=$\frac{{v}^{2}}{r}$知,向心加速度a与r成反比;由公式a=rω2可知,a与r成正比 | |
| C. | 向心加速度方向时刻在变化 | |
| D. | 向心加速度可能等于零 |
13.某同学发现有人触电,他应采取的措施是( )
| A. | 不假思索地去把触电人用手拉开 | B. | 当做没看见 | ||
| C. | 迅速找一根木棒,把人和电线分离 | D. | 立即大声喊人,让别人来处理 |
17. 如图所示,物体在光滑斜面上由静止开始下滑,在下滑过程中,以下说法正确的是( )
如图所示,物体在光滑斜面上由静止开始下滑,在下滑过程中,以下说法正确的是( )
 如图所示,物体在光滑斜面上由静止开始下滑,在下滑过程中,以下说法正确的是( )
如图所示,物体在光滑斜面上由静止开始下滑,在下滑过程中,以下说法正确的是( )| A. | 重力做正功 | B. | 重力做负功 | C. | 支持力做正功 | D. | 支持力做负功 |
18.下列说法中正确是( )
| A. | 物体体积增大时,其分子势能一定增大 | |
| B. | 只要物体温度升高,其分子平均动能就一定变大 | |
| C. | 空气绝对湿度不变时.温度越高,相对湿度越小 | |
| D. | 给自行车打气越打越困难,主要是因为气体分子间斥力越来越大 | |
| E. | 液体表面层分子比内部分子稀疏,因此液体表面有收缩的趋势 |
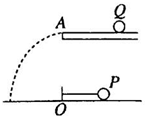 如图所示,小球P用长L=1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2πrad/s.另一质量m=1kg的小球Q放在高出水平面h=0.8m的光滑水平槽上,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,P球恰好在水平槽的正下方,水平槽与绳平行,Q运动到A时,力F自然取消(g取10m/s2).
如图所示,小球P用长L=1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2πrad/s.另一质量m=1kg的小球Q放在高出水平面h=0.8m的光滑水平槽上,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,P球恰好在水平槽的正下方,水平槽与绳平行,Q运动到A时,力F自然取消(g取10m/s2).