题目内容
18.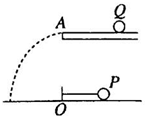 如图所示,小球P用长L=1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2πrad/s.另一质量m=1kg的小球Q放在高出水平面h=0.8m的光滑水平槽上,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,P球恰好在水平槽的正下方,水平槽与绳平行,Q运动到A时,力F自然取消(g取10m/s2).
如图所示,小球P用长L=1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω=2πrad/s.另一质量m=1kg的小球Q放在高出水平面h=0.8m的光滑水平槽上,槽口A点在O点正上方.当小球Q受到水平恒力F作用时,P球恰好在水平槽的正下方,水平槽与绳平行,Q运动到A时,力F自然取消(g取10m/s2).(1)恒力F的表达式为何值,两小球可能相碰?(用m,L,ω,h,g表示)
(2)在满足(1)条件的前提下,求Q运动到槽口的最短时间和相应的Q在槽上滑行的距离.
分析 (1)先根据牛顿第二定律和运动学公式表示出球Q到达A点的速度,然后由平抛运动规律表示出球Q平抛下落的时间,由圆周运动周期公式表示出P到达最左端的时间,列式时注意P球运动的周期性;
(2)P球运动半圈时有最短时间,由上题结果求解.
解答 解:(1)为了保证两球相碰,球Q从A点飞出水平射程为L,设飞出时的速度为v,则:
由牛顿第二定律:F=ma
球的速度:v=at
从A点飞出后做平抛运动:
L=vt′,
h=$\frac{1}{2}$gt′2
要使两球相碰应有:$\sqrt{\frac{2h}{g}}$+t=($\frac{1}{2}$+k)$\frac{2π}{ω}$
解以上各式得:F=$\frac{mgLω}{(2k+1)π\sqrt{2gh}-2hω}$,(k=0,1,2…)
(2)由(1)知k=0时t最短,tmin=0.1s
同时得:Fmin=25N
所以球Q在槽上滑行的距离为:x=$\frac{1}{2}•\frac{{F}_{min}}{m}{t}_{min}^{2}$=$\frac{1}{2}$×$\frac{25}{2}$×0.12=0.125m
答:(1)恒力F的表达式为F=$\frac{mgLω}{(2k+1)π\sqrt{2gh}-2hω}$,(k=0,1,2…),两小球可能相碰.
(2)在满足(1)条件的前提下,Q运动到槽口的最短时间是0.1s,相应的Q在槽上滑行的距离是0.125m.
点评 本题涉及了匀变速直线运动、圆周运动、平抛运动,根据不同的运动形式选择不同的运动规律,用时间相等将它们联系起来是关键.解题时要注意圆周运动的周期性.

练习册系列答案
相关题目
13. 如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )
如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )
 如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )
如图,沿水平面向右运动的物体,受到一水平拉力F=20N作用.已知物体与水平面的动摩擦因数μ=0.2,物体质量m=5kg,则物体所受摩擦力为(取g=10m/s2)( )| A. | 20N,水平向左 | B. | 20N,水平向右 | C. | 10N,水平向左 | D. | 10N,水平向右 |
14.“神九”载人飞船与“天宫一号”成功对接及“蛟龙”号下潜突破7000米入选2012年中国十大科技进展新闻.若地球半径为R,把地球看做质量分布均匀的球体(质量分布均匀的球壳对球内任一质点的万有引力为零).“蛟龙”号下潜深度为d,“天宫一号”轨道距离地面高度为h,“蛟龙”号所在处与“天宫一号”所在处的重力加速度之比为( )
| A. | $\frac{R-d}{R+h}$ | B. | $\frac{(R-d)^{2}}{(R+h)^{2}}$ | C. | $\frac{(R-d)(R+h)^{2}}{{R}^{3}}$ | D. | $\frac{(R-d)(R+h)}{{R}^{2}}$ |
6. 如图所示,一斜面固定在水平面上,斜面上的CD部分光滑,DE部分粗糙,A,B两物体叠放在一起,从顶端C点由静止下滑,下滑过程中A、B保持相对静止,且在DE段做匀速运动,已知A、B间的接触面水平,则( )
如图所示,一斜面固定在水平面上,斜面上的CD部分光滑,DE部分粗糙,A,B两物体叠放在一起,从顶端C点由静止下滑,下滑过程中A、B保持相对静止,且在DE段做匀速运动,已知A、B间的接触面水平,则( )
 如图所示,一斜面固定在水平面上,斜面上的CD部分光滑,DE部分粗糙,A,B两物体叠放在一起,从顶端C点由静止下滑,下滑过程中A、B保持相对静止,且在DE段做匀速运动,已知A、B间的接触面水平,则( )
如图所示,一斜面固定在水平面上,斜面上的CD部分光滑,DE部分粗糙,A,B两物体叠放在一起,从顶端C点由静止下滑,下滑过程中A、B保持相对静止,且在DE段做匀速运动,已知A、B间的接触面水平,则( )| A. | 沿CD部分下滑时,A的机械能减小,B的机械能增加,但总的机械能不变 | |
| B. | 沿CD部分下滑时,A的机械能增加,B的机械能减小,但总的机械能不变 | |
| C. | 沿DE部分下滑时,A的机械能不变,B的机械能减小,而总的机械能减小 | |
| D. | 沿DE部分下滑时,A的机械能减小,B的机械能减小,而总的机械能减小 |
3.下面的几个速度中表示瞬时速度的是( )
| A. | 子弹射出枪口的速度是800 m/s,以 790 m/s的速度击中目标 | |
| B. | 汽车从甲站行驶到乙站过程中的速度是40 km/h | |
| C. | 汽车通过站牌时的速度是72 km/h | |
| D. | 小球第3 s末的速度是6 m/s |
10. 两个带电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,如图所示,已知PC=CO=OH,取无穷远处电势为零,则下列结论中正确的有( )
两个带电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,如图所示,已知PC=CO=OH,取无穷远处电势为零,则下列结论中正确的有( )
 两个带电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,如图所示,已知PC=CO=OH,取无穷远处电势为零,则下列结论中正确的有( )
两个带电量相等的正点电荷分别固定于绝缘水平面上的A、B两点,A、B连线的垂直平分线上有P、C、O、H四点,如图所示,已知PC=CO=OH,取无穷远处电势为零,则下列结论中正确的有( )| A. | C点和H点的电场强度相同 | |
| B. | H点的场强大小一定大于P点场强大小 | |
| C. | 正的检验电荷q自C点由静止释放后,将向O点运动 | |
| D. | C点电势高于P点电势,且C点和P点的电势皆高于零 |
7.如图所示,物体A放在斜面上处于静止状态,则关于物体A受到的力,下列说法中正确的是( )


| A. | 受竖直向下的重力、垂直斜面向上的弹力、沿斜面向下的下滑力、沿斜面向上的摩擦力 | |
| B. | 受竖直向下的重力、垂直斜面向下的弹力、沿斜面向下的下滑力 | |
| C. | 受竖直向下的重力、垂直斜面向上的弹力、沿斜面向上的摩擦力 | |
| D. | 受竖直向下的重力、垂直斜面向下的弹力、沿斜面向下的摩擦力 |
8. 一个绕中心线AB以一定的角速度转动的圆环,P、Q为环上两点,位置如图所示,下列说法正确的是( )
一个绕中心线AB以一定的角速度转动的圆环,P、Q为环上两点,位置如图所示,下列说法正确的是( )
 一个绕中心线AB以一定的角速度转动的圆环,P、Q为环上两点,位置如图所示,下列说法正确的是( )
一个绕中心线AB以一定的角速度转动的圆环,P、Q为环上两点,位置如图所示,下列说法正确的是( )| A. | P、Q两点的角速度相等 | B. | P、Q两点的线速度相等 | ||
| C. | P、Q两点的角速度之比为$\sqrt{3}$:1 | D. | P、Q两点的线速度之比为1:1 |
 某同学用甲图装置做验证动量守恒定律的实验.先将A球从斜槽轨道上某固定点处由静止开始滚下,在水平地面上的记录纸上留下压痕,重复10次;再把同样大小的B球放在斜槽轨道末端水平段的最右端附近静止,让A球仍从原固定点由静止开始滚下,和B球相碰后,两球分别落在记录纸的不同位置处,重复10次.从左向右依次是MPN点
某同学用甲图装置做验证动量守恒定律的实验.先将A球从斜槽轨道上某固定点处由静止开始滚下,在水平地面上的记录纸上留下压痕,重复10次;再把同样大小的B球放在斜槽轨道末端水平段的最右端附近静止,让A球仍从原固定点由静止开始滚下,和B球相碰后,两球分别落在记录纸的不同位置处,重复10次.从左向右依次是MPN点