题目内容
如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上,若在转动过程中,皮带不打滑,则( )
A.a点与b点的线速度大小相等
B.a点与b点的角速度大小相等
C.a点与c点的线速度大小相等
D.a点与d点的向心加速度大小相等

【解题指南】求解此题应明确a、c两点线速度大小相等,b、c、d三点角速度大小相等,然后利用公式![]() 求解.
求解.
【解析】选C、D.vc=2rω,vb=rω,所以vc=2vb,a、c是皮带连接的两轮边缘上的点,线速度大小相等,所以va=2vb,故A错C对;va=rωa,vb=rωb,由va=2vb,得ωa=2ωb,故B错;设a点线速度为v,c点线速度也为v,对c点,v=2rω,对d点,![]() ,故a点与d点的向心加速度大小相等,D对.
,故a点与d点的向心加速度大小相等,D对.
【总结提升】传动问题的解题技巧
(1)明确皮带传动和轮轴的特点.
(2)清楚线速度、角速度、向心加速度与半径的关系,从而能熟练地运用在线速度或角速度相等时,角速度、线速度、加速度与半径的比值关系.
(3)同转轴上各点ω相同,而线速度v=ωr与半径成正比.
(4)不考虑皮带打滑的情况下,两轮边缘的各点线速度大小相等,而角速度![]() 与半径成反比.另外,由v、T、f、ω之间的关系,向心加速度的表达式
与半径成反比.另外,由v、T、f、ω之间的关系,向心加速度的表达式![]() ,在应用时,要结合已知条件灵活运用.
,在应用时,要结合已知条件灵活运用.

练习册系列答案
相关题目
 (2013?湖南模拟)如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
(2013?湖南模拟)如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )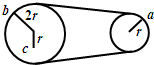 如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点;左轮的半径为2r,b是左轮边缘上的一点,c到左轮中心的距离为r.若在传动过程中,两轮均匀速率转动,且皮带不打滑.则a、b两点的线速度大小关系是va:vb=
如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点;左轮的半径为2r,b是左轮边缘上的一点,c到左轮中心的距离为r.若在传动过程中,两轮均匀速率转动,且皮带不打滑.则a、b两点的线速度大小关系是va:vb= 如图所示为一皮带传动装置,在传动过程中皮带不打滑,则轮上A、B、C三点的线速度、角速度及向心加速度的关系正确的是( )
如图所示为一皮带传动装置,在传动过程中皮带不打滑,则轮上A、B、C三点的线速度、角速度及向心加速度的关系正确的是( ) 如图所示为一皮带传动装置,右轮半径为r,a点在它的边缘上.左轮半径为2r,b点在它的边缘上.若在传动过程中,皮带不打滑,则a、b两点的角速度之比为ωa:ωb=
如图所示为一皮带传动装置,右轮半径为r,a点在它的边缘上.左轮半径为2r,b点在它的边缘上.若在传动过程中,皮带不打滑,则a、b两点的角速度之比为ωa:ωb= 如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左轮的半径为2r.c点在左轮上,到左轮中心的距离为r.a点和b点分别位于右轮和左轮的边缘上.若在传动过程中,皮带不打滑.则 ( )
如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左轮的半径为2r.c点在左轮上,到左轮中心的距离为r.a点和b点分别位于右轮和左轮的边缘上.若在传动过程中,皮带不打滑.则 ( )