题目内容
10. 如图所示,相距为R的两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向外的匀强磁场.D为收集板,收集板上各点到O点的距离以及两端点A和C的距离都为2R,板两端点的连线AC垂直M、N板.质量为m、带电量为+q的粒子,经s1进入M、N间的电场后,通过s2进入磁场.粒子在s1处的速度和粒子所受的重力均不计.
如图所示,相距为R的两块平行金属板M、N正对着放置,s1、s2分别为M、N板上的小孔,s1、s2、O三点共线,它们的连线垂直M、N,且s2O=R.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向外的匀强磁场.D为收集板,收集板上各点到O点的距离以及两端点A和C的距离都为2R,板两端点的连线AC垂直M、N板.质量为m、带电量为+q的粒子,经s1进入M、N间的电场后,通过s2进入磁场.粒子在s1处的速度和粒子所受的重力均不计.(1)当M、N间的电压为Ux时,求粒子进入磁场时速度的大小vx;
(2)要使粒子能够打在收集板上,求在M、N间所加电压的范围;
(3)若粒子恰好打在收集板D的中点上,求粒子从s1开始运动到打在D的中点上经历的时间.
分析 (1)粒子在电场中运动时,电场力做功引起动能变化,由动能定理vx;
(2)粒子进入磁场后,由洛伦兹力提供向心力做匀速圆周运动,由牛顿第二定律求出轨迹半径表达式.当粒子打在收集板D的A点时,轨迹半径最小,粒子速度最小,在M、N间所加电压最小;当粒子打在收集板D的C点时,轨迹半径最大,粒子速度最大,在M、N间所加电压最大;由几何知识求出半径,再求解电压的范围.
(3)粒子从s1开始运动到打在D的中点上经历的时间分三段:加速电场中,由运动学平均速度法求出时间;磁场中根据时间与周期的关系求解时间;射出磁场后粒子做匀速直线运动,由速度公式求解时间,再求解总时间.
解答 解:(1)粒子从s1到达s2的过程中,根据动能定理得:$q{U_x}=\frac{1}{2}m{v_x}^2$
解得:${v_x}=\sqrt{\frac{{2q{U_x}}}{m}}$
(2)粒子进入磁场后在洛伦兹力作用下做匀速圆周运动,设此时其速度大小为v,轨道半径为r,根据牛顿第二定律得:$qvB=m\frac{v^2}{r}$
粒子在M、N之间运动,根据动能定理得:$qU=\frac{1}{2}m{v^2}$,
联立解得:$U=\frac{{q{B^2}{r^2}}}{2m}$
当粒子打在收集板D的A点时,经历的时间最长,由几何关系可知粒子在磁场中运动的半径${r_1}=\frac{{\sqrt{3}}}{3}R$,此时M、N间的电压最小,为${U_1}=\frac{{q{B^2}{R^2}}}{6m}$
当粒子打在收集板D的C点时,经历的时间最短,由几何关系可知粒子在磁场中运动的半径${r_2}=\sqrt{3}R$,此时M、N间的电压最大,为${U_2}=\frac{{3q{B^2}{R^2}}}{2m}$
要使粒子能够打在收集板D上,在M、N间所加电压的范围为$\frac{{q{B^2}{R^2}}}{6m}≤U≤\frac{{3q{B^2}{R^2}}}{2m}$.
(3)根据题意分析可知,当粒子打在收集板D的中点上时,根据几何关系可以求得粒子在磁场中运动的半径r0=R,粒子进入磁场时的速度${v_0}=\frac{{qB{r_0}}}{m}$
粒子在电场中运动的时间:${t}_{1}=\frac{R}{\frac{{v}_{0}}{2}}$
粒子在磁场中做匀速圆周运动的周期$T=\frac{{2π{r_0}}}{v_0}=\frac{2πm}{qB}$
粒子在磁场中经历的时间${t_2}=\frac{1}{4}T$
粒子出磁场后做匀速直线运动经历的时间${t_3}=\frac{R}{v_0}$
所以粒子从s1运动到A点经历的时间为$t={t_1}+{t_2}+{t_3}=\frac{(6+π)m}{2qB}$
答:(1)当M、N间的电压为Ux时,粒子进入磁场时速度的大小${v_x}=\sqrt{\frac{{2q{U_x}}}{m}}$;
(2)要使粒子能够打在收集板D上,在M、N间所加电压的范围为$\frac{{q{B^2}{R^2}}}{6m}≤U≤\frac{{3q{B^2}{R^2}}}{2m}$;
(3)若粒子恰好打在收集板D的中点上,粒子从s1开始运动到打在D的中点上经历的时间是$\frac{(6+π)m}{2qB}$.
点评 本题是带电粒子先经电场加速,后经磁场偏转的问题,关键是根据几何知识分析粒子在磁场运动的半径与磁场半径的关系.

 图为μ氢原于(μ子与质子构成)的能级示意图.若用光子能量2360~2380ev范围内的光去照射大量处于基态的μ氢原子,根据玻尔理论.下列判断正确的是.( )
图为μ氢原于(μ子与质子构成)的能级示意图.若用光子能量2360~2380ev范围内的光去照射大量处于基态的μ氢原子,根据玻尔理论.下列判断正确的是.( )| A. | 照射光光子不可能被基态μ氢原于吸收 | |
| B. | 可能被基态μ氢原子吸收的不同频率的光子最多有6种 | |
| C. | 吸收照射光光子后的μ氢原子可辐射出不同频率的光子最多有3种 | |
| D. | 吸收照射光光子后的μ氢原子可辐射出不同频率的光子最多有6种 |
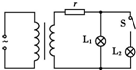 用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题.如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为r,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法正确的是( )
用电高峰期,电灯往往会变暗,其原理可简化为如下物理问题.如图所示,理想变压器副线圈上,通过输电线连接两只相同的灯泡L1和L2,输电线的等效电阻为r,原线圈输入有效值恒定的交流电压,当开关S闭合时,以下说法正确的是( )| A. | 原线圈中电流减小 | B. | r两端的电压增大 | ||
| C. | 原线圈输入功率不变 | D. | 副线圈输出电压减小 |
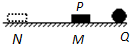 如图,在粗糙绝缘水平面上固定一点电荷Q,在M点无初速度地释放带电小物块P,P将沿水平面运动到N点静止,则从M到N的过程中( )
如图,在粗糙绝缘水平面上固定一点电荷Q,在M点无初速度地释放带电小物块P,P将沿水平面运动到N点静止,则从M到N的过程中( )| A. | P所受库仑力逐渐减小 | |
| B. | P的电势能一定增加 | |
| C. | M、N 两点的电势φM一定高于φN | |
| D. | 克服摩擦力做的功等于电势能的减少 |
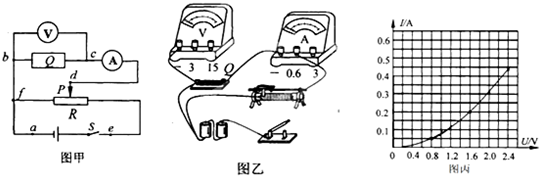
 用发光二极管制成的LED灯具有发光效率高、使用寿命长等优点,在生产与生活中得到广泛应用.某同学找到一个LED灯泡,研究它的特性,测得它两端电压U和通过的电流I,数据如表:
用发光二极管制成的LED灯具有发光效率高、使用寿命长等优点,在生产与生活中得到广泛应用.某同学找到一个LED灯泡,研究它的特性,测得它两端电压U和通过的电流I,数据如表:| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| U/V | 0.00 | … | … | … | 2.60 | 2.72 | 2.80 | 2.92 | 3.00 | 3.17 | 3.30 | 3.50 |
| I/mA | 0.00 | … | … | … | 1.29 | 5.77 | 8.71 | 19.05 | 27.30 | 38.86 | 50.63 | 68.00 |
A.电流表(量程0-0.6A,内阻约1Ω)
B.电流表(量程0-100mA,内阻约50Ω)
C.电压表(量程0-6V,内阻约50kΩ)
D.电压表(量程0-15V,内阻约60kΩ)
E.电源(电动势6V,内阻不计)
F.滑动变阻器(阻值范围0-10Ω,允许最大电流3A)
G.开关,导线
该同学做实验时,电压表选用的是C,电流表选用的是B(填选项字母);
②请在如图中以笔划线代替导线,按实验要求将实物图中的连线补充完整;
③开关S闭合之前,图中滑动变阻器的滑片应该置于A(选填“A端”、“B端”或“AB正中间”).
④若该LED灯泡的额定电压为3V,则此LED灯泡的额定功率为8.19×10-2W.
 某同学为了测量一个额定率为1W的电阻Rx的阻值,先多用表的欧姆档进行了粗测,然后用伏安法进行精确测量.
某同学为了测量一个额定率为1W的电阻Rx的阻值,先多用表的欧姆档进行了粗测,然后用伏安法进行精确测量. 玉树地震发生后,需要向灾区运送大量救灾物资,在物资转运过程中常使用如图所示的传送带.已知某传送带与水平面成θ=37°角,传送带的AB部分长L=5.8m,传送带以恒定的速率v=4m/s按图示方向传送,若在B端无初速度地放置一个质量m=50kg的救灾物资P(可视为质点),P与传送带之间的动摩擦因数μ=0.5(取g=10m/s2,sin37°=0.6).求:
玉树地震发生后,需要向灾区运送大量救灾物资,在物资转运过程中常使用如图所示的传送带.已知某传送带与水平面成θ=37°角,传送带的AB部分长L=5.8m,传送带以恒定的速率v=4m/s按图示方向传送,若在B端无初速度地放置一个质量m=50kg的救灾物资P(可视为质点),P与传送带之间的动摩擦因数μ=0.5(取g=10m/s2,sin37°=0.6).求: