题目内容
16. 如图甲所示是游乐场中过山车的实物图片,可将过山车的一部分运动简化为图乙的模型图.模型图中光滑圆形轨道的半径R=8.0m,该光滑圆形轨道固定在倾角为θ=37°的斜轨道面上的Q点,圆形轨道的最高点A与倾斜轨道上的P点平齐,圆形轨道与斜轨道之间平滑连接.现使质量为m=50kg的小车(视作质点)从P点以一定的初速度v0=12m/s沿斜面向下运动,不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A.
如图甲所示是游乐场中过山车的实物图片,可将过山车的一部分运动简化为图乙的模型图.模型图中光滑圆形轨道的半径R=8.0m,该光滑圆形轨道固定在倾角为θ=37°的斜轨道面上的Q点,圆形轨道的最高点A与倾斜轨道上的P点平齐,圆形轨道与斜轨道之间平滑连接.现使质量为m=50kg的小车(视作质点)从P点以一定的初速度v0=12m/s沿斜面向下运动,不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A.(1)小车在A点的速度为多大?
(2)小车在圆形轨道上运动时对轨道的最大压力为多少?
(3)求斜轨道面与小车间的动摩擦因数为多大?
分析 (1)小车恰好能通过圆形轨道的最高点A处,轨道对小车的弹力为零,由重力提供小车圆周运动所需要的向心力,根据牛顿第二定律求出小车在A点的速度.
(2)根据动能定理或机械能守恒求出小车在轨道B点是的速度,再运用牛顿第二定律,通过支持力和重力的合力提供向心力,求出支持力,由牛顿第三定律得到压力.
(3)对P到A全过程运用动能定理,重力做功为零,根据几何关系求出在斜面上的位移,通过动能定理求出动摩擦因数.
解答  解:(1)由于小车恰能通过A点,由重力提供小车圆周运动所需要的向心力,根据牛顿第二定律得:
解:(1)由于小车恰能通过A点,由重力提供小车圆周运动所需要的向心力,根据牛顿第二定律得:
mg=m$\frac{{v}_{A}^{2}}{R}$
解得:vA=$\sqrt{gR}$=4$\sqrt{5}$ m/s.①
(2)如图,小车经轨道最低点D时对轨道压力最大.设在D点轨道对小车的支持力为N
则有:N-mg=m$\frac{{v}_{D}^{2}}{R}$②
小车由D到A的运动过程机械能守恒
则有:2mgR=$\frac{1}{2}$mv${\;}_{D}^{2}$-$\frac{1}{2}$mv${\;}_{A}^{2}$ ③
由①②③得:N=6mg.
由牛顿第三定律,在D点小车对轨道的压力N′=N=6mg=3000N.
(3)设PQ距离为L,对小车由P到A的过程应用动能定理
得:-μmgLcos37°=$\frac{1}{2}$mv${\;}_{A}^{2}$-$\frac{1}{2}$mv${\;}_{0}^{2}$④
由几何关系:L=$\frac{R+Rcos37°}{sin37°}$⑤
由①④⑤得:μ=$\frac{1}{6}$.
答:
(1)小车在A点的速度为4$\sqrt{5}$m/s.
(2)小车在圆形轨道运动时对轨道的最大压力为6mg.
(3)斜轨道面与小车间的动摩擦因数是$\frac{1}{6}$.
点评 本题综合考查了牛顿第二定律和动能定理,关键是理清运动的过程,运用合适的规律进行求解.

| A. | 速度 | B. | 动能 | C. | 动量 | D. | 总能量 |
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{16}{7}$ |
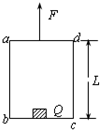 如图所示,在高为L的木箱abcd的底部放有一个小物体Q(可视为质点),现用力F向上拉绳,使木箱由静止开始运动,若保持拉力的功率不变,经过t时间,木箱达到最大速度,这时让木箱实然停止,小物体由于惯性会继续向上运动,且恰能达到木箱顶端.若重力加速度为g,空气阻力不计,以下说法正确的是( )
如图所示,在高为L的木箱abcd的底部放有一个小物体Q(可视为质点),现用力F向上拉绳,使木箱由静止开始运动,若保持拉力的功率不变,经过t时间,木箱达到最大速度,这时让木箱实然停止,小物体由于惯性会继续向上运动,且恰能达到木箱顶端.若重力加速度为g,空气阻力不计,以下说法正确的是( )| A. | 木箱即将达到最大速度之前,物体Q处于超重状态 | |
| B. | 木箱突然停止运动时,物体Q处于超重状态 | |
| C. | 木箱的最大速度为$\sqrt{2gL}$ | |
| D. | 可以确定t时间内木箱上升的高度 |
| A. | “神舟”八号绕地球正常飞行时宇航员的加速度小于9.8m/s2 | |
| B. | “神舟”八号绕地球正常飞行的速率可能大于8km/s | |
| C. | “神舟”八号飞船在轨道上正常飞行时,宇航员处于完全失重状态 | |
| D. | “神舟”八号运行的周期比地球近地卫星的周期大 |
 船在静水中的速度与时间的关系如图(甲)所示.河宽300m,河水的流速与船离一侧河岸的距离的变化关系如图(乙)所示,则( )
船在静水中的速度与时间的关系如图(甲)所示.河宽300m,河水的流速与船离一侧河岸的距离的变化关系如图(乙)所示,则( )| A. | 船渡河的最短时间100s | |
| B. | 要使船以最短时间渡河,船在行驶过程中,船头必须始终与河岸垂直 | |
| C. | 船在河水中航行的轨迹是一条直线 | |
| D. | 船在河水中的最大速度是5m/s |
| A. | 能产生光电效应时,光电流大小随入射光强度增大而增加 | |
| B. | 某种光照射金属时,能产生光电效应,则入射光强度越大,光电子从金属内逸出所需时间越短 | |
| C. | 对某种金属来说,入射光的波长必须大于某个值,才能产生光电效应 | |
| D. | 对某种金属来说,入射光的频率越大,对应的遏止电压越大 |
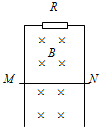 如图所示,MN为金属杆,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有电阻R=0.5Ω,导轨与金属杆的电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN稳定下滑时,每秒钟有0.02J的重力势能转化为电能,求
如图所示,MN为金属杆,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距l=10cm,导轨上端接有电阻R=0.5Ω,导轨与金属杆的电阻不计,整个装置处于B=0.5T的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆MN稳定下滑时,每秒钟有0.02J的重力势能转化为电能,求