题目内容
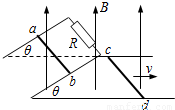
 光滑平行导轨弯成如图所示形状,倾斜部分与水平部分之间夹角为θ,圆周部分半径为R.匀强磁场只限于水平部分如图虚线内很窄的区域,磁感应强度为B,方向竖直向上.导体棒2位于磁场右边界,将导体棒1在倾斜导轨部分高h处由静止释放,棒1和2质量均为m,电阻均为R且始终与导轨垂直,棒2刚好能滑到圆弧轨道的最高点,不计棒在倾斜导轨和水平导轨连接处的能量损失.则导体棒2在离开磁场的瞬间过程中回路内产生的电能.
光滑平行导轨弯成如图所示形状,倾斜部分与水平部分之间夹角为θ,圆周部分半径为R.匀强磁场只限于水平部分如图虚线内很窄的区域,磁感应强度为B,方向竖直向上.导体棒2位于磁场右边界,将导体棒1在倾斜导轨部分高h处由静止释放,棒1和2质量均为m,电阻均为R且始终与导轨垂直,棒2刚好能滑到圆弧轨道的最高点,不计棒在倾斜导轨和水平导轨连接处的能量损失.则导体棒2在离开磁场的瞬间过程中回路内产生的电能.分析:对2棒,在最高处,根据牛顿第二定律求得对应的速度,从最低处到最高处,由动能定理求得最低处的速度.
对1棒,由动能定理列出等式,对1棒和2棒,由动量守恒列出等式.由系统能量守恒求解产生的电能.
对1棒,由动能定理列出等式,对1棒和2棒,由动量守恒列出等式.由系统能量守恒求解产生的电能.
解答:解:对2棒,在最高处,根据牛顿第二定律得:mg=
从最低处到最高处,由动能定理得:
-2mgR=
-
得:v2=
对1棒,由动能定理得:
mgh=
得:v0=
对1棒和2棒,由动量守恒得:mv0=mv1+mv2
得:v1=
-
棒2在离开磁场的瞬间过程中回路内产生的电能,可由系统能量守恒得:
E电=
-(
-
)=mg
-5mgR
答:导体棒2在离开磁场的瞬间过程中回路内产生的电能是mg
-5mgR.
| ||
| R |
从最低处到最高处,由动能定理得:
-2mgR=
| ||
| 2 |
| ||
| 2 |
得:v2=
| 5gR |
对1棒,由动能定理得:
mgh=
| ||
| 2 |
得:v0=
| 2gh |
对1棒和2棒,由动量守恒得:mv0=mv1+mv2
得:v1=
| 2gh |
| 5gR |
棒2在离开磁场的瞬间过程中回路内产生的电能,可由系统能量守恒得:
E电=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 10hR |
答:导体棒2在离开磁场的瞬间过程中回路内产生的电能是mg
| 10hR |
点评:本题主要考查了牛顿第二定律、动能定理、动量守恒定律和能量守恒的应用,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.有两导体棒ab和cd,质量均为m,两导体棒的电阻与固定电阻R阻值相等(阻值未知),垂直于导轨放置,且与导轨间接触良好,当导体棒cd沿底部导轨向右滑动速度为v时,导体棒ab恰好在倾斜导轨上处于静止状态,则此时( )
如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.有两导体棒ab和cd,质量均为m,两导体棒的电阻与固定电阻R阻值相等(阻值未知),垂直于导轨放置,且与导轨间接触良好,当导体棒cd沿底部导轨向右滑动速度为v时,导体棒ab恰好在倾斜导轨上处于静止状态,则此时( )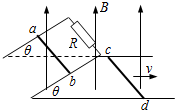 如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.导体棒ab和cd,质量均为m,垂直于导轨放置,且与导轨间接触良好,两导体棒的电阻与固定电阻R阻值相等,其余部分电阻不计,当导体棒cd沿底部导轨向右以速度为v匀速滑动时,导体棒ab恰好在倾斜导轨上处于静止状态,则导体棒ab消耗的热功率与cd棒克服安培力做功的功率之比为
如图所示,间距为L的光滑平行金属导轨弯成“∠”型,底部导轨面水平,倾斜部分与水平面成θ角,导轨与固定电阻R相连,整个装置处于竖直向上的大小为B的匀强磁场中.导体棒ab和cd,质量均为m,垂直于导轨放置,且与导轨间接触良好,两导体棒的电阻与固定电阻R阻值相等,其余部分电阻不计,当导体棒cd沿底部导轨向右以速度为v匀速滑动时,导体棒ab恰好在倾斜导轨上处于静止状态,则导体棒ab消耗的热功率与cd棒克服安培力做功的功率之比为