题目内容
17.体育课上同学们进行了一项抛球入框游戏,球框(框壁厚忽略不计)紧靠竖直墙壁放在水平地面上,如图所示,某同学将球(可视为质点)正对竖直墙壁水平抛出并投入框中,球框高度和球框左侧壁离墙壁的距离均为L=0.4m,球的抛出点离地面的高度H=1.2m,离墙壁的水平距d=2.0m,球与墙壁碰撞前后瞬间速度大小相等,方向关于墙壁对称,求:g=10m/s2,空气阻力不计,求:(1)为使球落入框中,球抛出时的最小速度;
(2)为使球落入框中,球与墙壁碰撞的最高点离地面的高度;
(3)若水平抛出的高度可以任意调整,为让小球入框口时的动能最小,则球水平抛出时的高度.
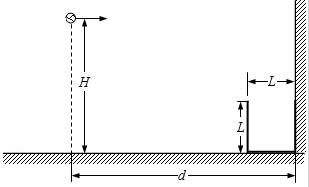
分析 (1)考虑临界情况,速度最小时恰好落在框的左上角,结合平抛运动的分位移公式列式求解初速度;
(2)球与墙壁碰撞类似于光的反射,具有对称性,根据平抛运动的规律和对称性求解;
(3)为让小球入框口时的动能最小,抛到框的左上角,结合平抛运动的分运动公式列式,再结合机械能守恒定律列式,联立得到入框口时的动能的表达式进行分析即可.
解答 解:(1)设球抛出时的最小速度为v,运动到框左侧上边缘的时间为t,则
H-L=$\frac{1}{2}$gt2
d-L=vt
联立解得:
$v=(d-L)\sqrt{\frac{g}{2(H-L)}}=(2-0.4)×\sqrt{\frac{10}{2×(1.2-0.4)}}m/s=4m/s$
(2)设球与墙壁碰撞的最高点离地面的高度为hmax,运动到墙壁的时间为t′,反弹到左上角的时间为t,根据平抛运动的分位移公式,由对称关系有:
d+L=vmaxt
H-L=$\frac{1}{2}g{t}^{2}$
解得:vmax=6m/s
从抛出到碰撞到墙壁过程,有:
vmaxt′=d
hmax=H-$\frac{1}{2}$g t′2
联立解得:hmax=1.2-$\frac{5}{9}$m≈0.64m
(3)设从y高度抛出,抛出到框的左上角,根据平抛运动的分运动公式,有:
y-L=$\frac{1}{2}g{t}^{2}$
d-L=v0t
解得:${v_0}=(d-L)\sqrt{\frac{g}{2(y-L)}}$
以地面为参考面,根据机械能守恒定律,有:$\frac{1}{2}m{v}_{0}^{2}+mgy={E}_{k}+mgL$
联立解得:${E_k}=\frac{6.4m}{y-0.4}+10m(y-0.4)≥2\sqrt{\frac{6.4m}{y-0.4}}\sqrt{10m(y-0.4)}=16m$
当$\sqrt{\frac{6.4m}{y-0.4}}=\sqrt{10m(y-0.4)}$,即y=1.2m时取最小值;
答:(1)为使球落入框中,球抛出时的最小速度为4m/s;
(2)为使球落入框中,球与墙壁碰撞的最高点离地面的高度为0.64m;
(3)若水平抛出的高度可以任意调整,为让小球入框口时的动能最小,则球水平抛出时的高度为1.2m.
点评 本题要掌握平抛运动的处理方法:运动的分解法,将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动,掌握运动学公式解题,关键抓住碰撞过程的对称性,理清两个方向的分位移.

| A. | 紫外线有灭菌消毒作用 | |
| B. | 紫外线能使荧光物质发光 适当的紫外线照射,有助于人体合成维生素 | |
| C. | 对骨骼的生长和身体的健康等许多方面都有好处 | |
| D. | 紫外线对人类总是有益的 |
 如图所示,P、Q两物块叠放在一起,以相同的初速度竖直向下抛出.若P的质量大于Q的质量,不计空气阻力,则在物块下降过程中,下列说法正确的是( )
如图所示,P、Q两物块叠放在一起,以相同的初速度竖直向下抛出.若P的质量大于Q的质量,不计空气阻力,则在物块下降过程中,下列说法正确的是( )| A. | Q所受的合外力等于Q受到的重力 | B. | Q所受的合外力小于Q受到的重力 | ||
| C. | P对Q的压力大于Q对P的支持力 | D. | P、Q间的弹力为零 |
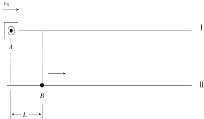 小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )
小明在某游乐训练场上练习移动打靶,如图所示,耙在Ⅰ号直线上以v0=10m/s的速度匀速向右移动,t1=0时刻耙在Ⅰ号直线上的A位置,在水平直线Ⅱ上距耙心水平距离L=25m的B处,小明坐在战车上从静止开始以a=2m/s2的加速度沿直线Ⅱ向右做匀加速直线运动,战车上的彩弹枪在战车静止时发出的彩弹速度v1=50m/s,Ⅰ、Ⅱ号水平直线的距离d=50m,sin37°=0.6.则( )| A. | 欲使彩弹击中耙心,可在t=5.0s时发出彩弹 | |
| B. | 若彩弹在最短时间内击中靶心,则击中靶心时彩弹的速度是50m/s | |
| C. | 若要求在t=10.0s时发出彩弹并击中靶心,则彩弹枪与Ⅱ号水平直线的夹角(锐角)是53° | |
| D. | 若要求在t=10.0s时发出彩弹并击中靶心,则彩弹飞行的时间是0.5s |
 桌面上放着一个单匝线圈,线圈中心上方一定高度有一竖直放置的条形磁铁,此时线圈内的磁通量为0.04Wb;把条形磁铁竖放在线圈内的桌面上时,线圈内的磁通量为0.12Wb;当把条形磁铁从该位置在0.1s内放到线圈内的桌面上的过程中,产生的感应电动势大小?
桌面上放着一个单匝线圈,线圈中心上方一定高度有一竖直放置的条形磁铁,此时线圈内的磁通量为0.04Wb;把条形磁铁竖放在线圈内的桌面上时,线圈内的磁通量为0.12Wb;当把条形磁铁从该位置在0.1s内放到线圈内的桌面上的过程中,产生的感应电动势大小?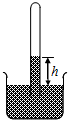 如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体压强为p,管内外水银面高度差为h.若增大外界大气压强,则h将增大(增大、减小、不变);p将增大(增大、减小、不变)
如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体压强为p,管内外水银面高度差为h.若增大外界大气压强,则h将增大(增大、减小、不变);p将增大(增大、减小、不变)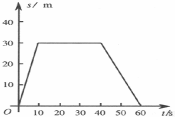 如图的x-t图象.0-10s物体做匀速直线运动,这段时间内物体的速度3m/s,10-40s物体静止,40-60s物体做匀速直线运动.这段时间里的速度为-3m/s.
如图的x-t图象.0-10s物体做匀速直线运动,这段时间内物体的速度3m/s,10-40s物体静止,40-60s物体做匀速直线运动.这段时间里的速度为-3m/s.