题目内容
质量为M的物块A以速度v运动,与质量为m的静止物块B发生正碰,碰撞后A的动量大小正好是B的动量大小的两倍,则两者的质量之比
可能为( )
| M |
| m |
分析:两物块发生正撞时动量守恒,又碰撞后A的动量大小正好是B的动量大小的两倍,求出质量为m的物块与初速V之间的关系,再结合碰撞时,机械能不能增加,即可求解.
解答:解:碰撞时动量守恒,故Mv=mv1+Mv2
又碰撞后A的动量大小正好是B的动量大小的两倍,
2mv1=Mv2 ①
则 v2=
v
又碰撞时,机械能不能增加,则有:
Mv2≥
m
+
M
②
由①②化简整理得M≥2m
即2≤
≤5
故选BC.
又碰撞后A的动量大小正好是B的动量大小的两倍,
2mv1=Mv2 ①
则 v2=
| 2 |
| 3 |
又碰撞时,机械能不能增加,则有:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
由①②化简整理得M≥2m
即2≤
| M |
| m |
故选BC.
点评:本题考查的是动量定律得直接应用,注意碰撞时,机械能不能增加,难度适中,属于中档题.

练习册系列答案
相关题目
 如图所示,质量为2kg的物块A(可看作质点),开始放在长木板B的左端,B的质量为1kg,可在水平面上无摩擦滑动,水平地面上有两个固定的竖直挡板M N,现A、B以相同的速度v0=6m/s向左运动并与挡板M发生碰撞.B 与M碰后速度立即变为零,但不与M粘接;A与M碰撞没有能量损失,碰后接着返向N板运动,且在与N板碰撞之前,A、B均能达到共同速度并且立即被锁定,与N板碰撞后A、B一并原速反向,并且立刻解除锁定.A、B之间的动摩擦因数μ=0.1.通过计算回答下列问题:g取10m/s2
如图所示,质量为2kg的物块A(可看作质点),开始放在长木板B的左端,B的质量为1kg,可在水平面上无摩擦滑动,水平地面上有两个固定的竖直挡板M N,现A、B以相同的速度v0=6m/s向左运动并与挡板M发生碰撞.B 与M碰后速度立即变为零,但不与M粘接;A与M碰撞没有能量损失,碰后接着返向N板运动,且在与N板碰撞之前,A、B均能达到共同速度并且立即被锁定,与N板碰撞后A、B一并原速反向,并且立刻解除锁定.A、B之间的动摩擦因数μ=0.1.通过计算回答下列问题:g取10m/s2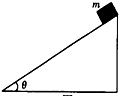 如图甲所示,斜面体固定在水平面上,倾角为θ=30°,质量为m的物块从斜面体上由静止释放,以加速度a=
如图甲所示,斜面体固定在水平面上,倾角为θ=30°,质量为m的物块从斜面体上由静止释放,以加速度a=