题目内容
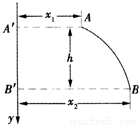
 某同学做平抛实验时,只在纸上记下重垂线y方向,未在纸上记下斜槽末端位置,并只描出如图所示的一段平抛运动曲线,现在曲线上取A、B两点,用刻度尺分别量出到y的距离,AA′=x1,BB′=
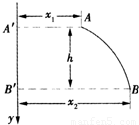
某同学做平抛实验时,只在纸上记下重垂线y方向,未在纸上记下斜槽末端位置,并只描出如图所示的一段平抛运动曲线,现在曲线上取A、B两点,用刻度尺分别量出到y的距离,AA′=x1,BB′=x2,以及AB的竖直距离h,从而求出小球被抛出时的初速度v0为
A
A
A.
|
|
C.
| x2+x1 |
| 2 |
|
| (x2-x1) |
| 2 |
|
分析:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,设初速度为v0,根据水平方向上的位移x1和x2,得出抛出点运动到A和B的时间,根据竖直方向上的距离差为h,求出初速度.
解答:解:设初速度为v0,则从抛出点运动到A所需的时间t1=
,从抛出点运动到B所需的时间t2=
,在竖直方向上有:
gt22-
gt12=h,代入t1、t2,解得v0=
.故A正确,B、C、D错误.
故选A.
| x1 |
| v0 |
| x2 |
| v0 |
| 1 |
| 2 |
| 1 |
| 2 |
|
故选A.
点评:解决本题的关键掌握处理平抛运动的方法,平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 在《研究平抛物体的运动》实验中,安装实验装置时轨道末端应注意保持
在《研究平抛物体的运动》实验中,安装实验装置时轨道末端应注意保持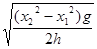 B.
B.
 D.
D.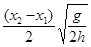
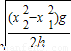 B.
B.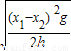
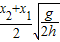 D.
D.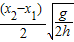 .
.
 B.
B.
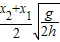 D.
D.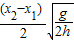 .
.