题目内容
6．
小球从h=1.8m高处以1m/s的速度水平抛出，在抛出点正前方0.4m处固定有一光滑竖直平板，小球与平板发生碰撞前后，水平分速度大小不变、方向相反，竖直分速度保持不变．求小球第一次的落地点与抛出点间的水平间距为多少？（g取10m/s2）
分析 将小球的运动分解为水平方向和竖直方向上，根据高度求出整个过程的运动时间，结合水平方向上速度大小不变，求出小球第一次的落地点与抛出点间的水平间距．
解答 解：根据h=$\frac{1}{2}g{t}^{2}$得，t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1.8}{10}}s=0.6s$，
则x=v0t=1×0.6m=0.6m，
则距离抛出点的水平间距△x=0.4-（0.6-0.4）m=0.2m．
答：小球第一次的落地点与抛出点间的水平间距为0.2m．
点评 解决本题的关键知道小球在水平方向和竖直方向上的运动规律，抓住等时性，结合运动学公式灵活求解．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
一辆汽车在平直的公路上以某一初速度运动，运动过程中保持恒定的牵引功率，其加速度a和速度的倒数（$\frac{1}{v}$）图象如图所示．若已知汽车的质量为2t，则根据图象所给的信息，求得汽车行驶的最大速度为20m/s，汽车保持的恒定功率为8×104W．
17．
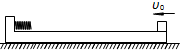如图所示，一块质量为M的木板停在光滑的水平面上，木板的左端有挡板，挡板上固定一个小弹簧．一个质量为m的小物块（可视为质点）以水平速度υ0从木板的右端开始向左运动，与弹簧碰撞后（弹簧处于弹性限度内），最终又恰好停在木板的右端．根据上述情景和已知量，可以求出（ ）
如图所示，一块质量为M的木板停在光滑的水平面上，木板的左端有挡板，挡板上固定一个小弹簧．一个质量为m的小物块（可视为质点）以水平速度υ0从木板的右端开始向左运动，与弹簧碰撞后（弹簧处于弹性限度内），最终又恰好停在木板的右端．根据上述情景和已知量，可以求出（ ）| A． | 弹簧的劲度系数 | |
| B． | 弹簧的最大弹性势能 | |
| C． | 木板和小物块组成的系统最终损失的机械能 | |
| D． | 若再已知木板长度l可以求出木板和小物块间的动摩擦因数 |
1．
如图所示，在一个顶角为2θ（θ=53°）的倒立的光滑圆锥面内，放有质量为m=1kg的小物体，小物体与竖直转轴OO’之间用与圆锥母线平行、长为L=1m的轻质细线相连．欲使细线不松弛，小物体随圆锥面一起做匀速圆周运动的角速度ω可以为（ ）（g取10m/s2，sin53°=0.8）
如图所示，在一个顶角为2θ（θ=53°）的倒立的光滑圆锥面内，放有质量为m=1kg的小物体，小物体与竖直转轴OO’之间用与圆锥母线平行、长为L=1m的轻质细线相连．欲使细线不松弛，小物体随圆锥面一起做匀速圆周运动的角速度ω可以为（ ）（g取10m/s2，sin53°=0.8）| A． | 2rad/s | B． | 3rad/s | C． | 4rad/s | D． | 5rad/s |
11．设同步卫星离地心的距离为r，运行速率为v1，加速度为a1；地球赤道上的物体随地球自转的向心加速度为a2，第一宇宙速度为v2，地球的半径为R，则下列比值正确的是（ ）
| A． | $\frac{v_1}{v_2}=\sqrt{\frac{r}{R}}$ | B． | $\frac{a_1}{a_2}=\frac{r^2}{R^2}$ | C． | $\frac{a_1}{a_2}=\frac{R^2}{r^2}$ | D． | $\frac{v_1}{v_2}=\sqrt{\frac{R}{r}}$ |
18．关于合运动与两个分运动的关系，下列说法正确的是（ ）
| A． | 合运动的速度一定大于任一个分运动的速度 | |
| B． | 合运动的速度可能小于任一个分运动的速度 | |
| C． | 合运动的方向就是物体实际运动的方向 | |
| D． | 两个分运动的时间一定和它们合运动的时间相等 |
（1）在“研究平抛运动”实验时，要求斜槽装置末端的切线必须是水平的，这样
16．下列各组物理量中，全部是矢量的一组是（ ）
| A． | 速度、速率、平均速度 | B． | 位移、速度、平均速度 | ||
| C． | 速度、加速度、路程 | D． | 力、速度、加速度 |