题目内容
19.如图所示,绝热气缸A和绝热气缸B固定在水平面上,气缸A和B中分别用活塞封闭一定质量的理想气体,活塞面积之比为SA:SB=1:2.两活塞用刚性细杆相连,可沿水平方向无摩擦滑动,两个气缸都不漏气.初始时,两气缸内装有压强为P0的理想气体,A、B中气体的体积皆为V0,温度皆为T0,P0是气缸外的大气压强值,设环境温度始终保持不变,现对A缓慢加热,使其压强升到PA=2.0P0时,求:
①此时气缸A中气体的体积VA;
②此时气缸A中气体的温度TA.
分析 由平衡条件求出气体的压强,应用理想气体的状态方程分别对A、B气体列方程,然后解方程求出气体A的温度
解答 解:(1)末态时活塞平衡,有:
${p}_{0}^{\;}{S}_{A}^{\;}+{p}_{B}^{\;}{S}_{B}^{\;}={p}_{A}^{\;}{S}_{A}^{\;}+{p}_{0}^{\;}{S}_{B}^{\;}$
${S}_{A}^{\;}:{S}_{B}^{\;}=1:2$,${p}_{A}^{\;}=2.0{p}_{0}^{\;}$
${p}_{B}^{\;}=\frac{3{p}_{0}^{\;}}{2}$
B中气体初、末态温度相等
初状态:${p}_{B1}^{\;}={p}_{0}^{\;}$,${V}_{B1}^{\;}={V}_{0}^{\;}$
末状态:${p}_{B2}^{\;}=\frac{3{p}_{0}^{\;}}{2}$,${V}_{B2}^{\;}=?$
由玻意耳定律得${p}_{B1}^{\;}{V}_{B1}^{\;}={p}_{B2}^{\;}{V}_{B2}^{\;}$
可求得${V}_{B2}^{\;}=\frac{2{V}_{0}^{\;}}{3}$
设A中气体末状态的体积为${V}_{A2}^{\;}$,因为两活塞移动的距离相等,故有
$\frac{{V}_{A2}^{\;}-{V}_{0}^{\;}}{{S}_{A}^{\;}}=\frac{{V}_{0}^{\;}-{V}_{B2}^{\;}}{{S}_{B}^{\;}}$
可求得${V}_{A2}^{\;}=\frac{7}{6}{V}_{0}^{\;}$
对气体A根据理想气体状态方程$\frac{pV}{T}=C$
解得${T}_{A2}^{\;}=\frac{{p}_{A2}^{\;}{V}_{A2}^{\;}}{{p}_{A1}^{\;}{V}_{A1}^{\;}}{T}_{A1}^{\;}=\frac{7}{3}{T}_{0}^{\;}$
答:①此时气缸A中气体的体积${V}_{A}^{\;}$为$\frac{7}{6}{V}_{0}^{\;}$;
②此时气缸A中气体的温度${T}_{A}^{\;}$为$\frac{7}{3}{T}_{0}^{\;}$.
点评 本题是连接体问题,找出两部分气体状态参量间的关系,然后由理想气体状态方程即可解题,要掌握连接体问题的解题思路与方法

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
| A. | A、B之间无摩擦力 | B. | A受到的摩擦力水平向右 | ||
| C. | B与地面之间无摩擦力 | D. | 地面对B的摩擦力水平向右 |
 如图所示,在匀速转动的圆筒内壁上,有一物体随圆筒一起转动而未滑动,下列正确的是( )
如图所示,在匀速转动的圆筒内壁上,有一物体随圆筒一起转动而未滑动,下列正确的是( )| A. | 物体受重力、向心力、摩擦力三个力 | B. | 物体受重力、弹力、向心力、摩擦力 | ||
| C. | 物体受重力、弹力、向心力三个力 | D. | 物体受重力、弹力、摩擦力三个力 |
 如图所示,曲线Ⅰ是一颗卫星绕地球做匀速圆周运动的轨道,其半径为R,曲线Ⅱ是另一颗卫星绕地球做椭圆运动的轨道,O点为地球的地心,AB为椭圆的长轴,两轨道和地心都在同一平面内,已知两卫星在轨道上运动的周期相等,万有引力常量为G,地球质量为M,则下列说法正确的是( )
如图所示,曲线Ⅰ是一颗卫星绕地球做匀速圆周运动的轨道,其半径为R,曲线Ⅱ是另一颗卫星绕地球做椭圆运动的轨道,O点为地球的地心,AB为椭圆的长轴,两轨道和地心都在同一平面内,已知两卫星在轨道上运动的周期相等,万有引力常量为G,地球质量为M,则下列说法正确的是( )| A. | 椭圆轨道的长轴长度为4R | |
| B. | 卫星在Ⅰ轨道上加速度大小为a0,卫星在Ⅱ轨道上经B点时加速度大小为aB,则有a0<aB | |
| C. | 卫星在Ⅰ轨道上速率为v0,卫星在Ⅱ轨道上经B点时速率为vB,则v0>vB | |
| D. | 若OA=0.4R,则卫星经B点时速率vB<$\sqrt{\frac{2GM}{3R}}$ |
| A. | 10W | B. | 100W | C. | 1kW | D. | 10 kW |
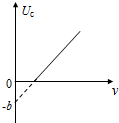 在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )| A. | 普朗克常量可表示为$\frac{k}{e}$ | |
| B. | 若更换材料再实验,得到的图线的k不改变,b改变 | |
| C. | 所用材料的逸出功可表示为eb | |
| D. | b由入射光决定,与所用材料无关 |
 如图甲所示,一上端开口、下端封闭的细长玻璃管竖直放置,管长为L,管里一段长$\frac{1}{3}$L的水银柱封住一段长$\frac{1}{3}$L的气体,大气压强为p0,温度为T0,现通过降低空气温度,使水银柱下降$\frac{1}{6}$L.求:
如图甲所示,一上端开口、下端封闭的细长玻璃管竖直放置,管长为L,管里一段长$\frac{1}{3}$L的水银柱封住一段长$\frac{1}{3}$L的气体,大气压强为p0,温度为T0,现通过降低空气温度,使水银柱下降$\frac{1}{6}$L.求: 发卡弯是形容赛道上某个弯角程度的词,比较形象.发卡弯一般的角度都接近180°.赛车过这种弯道的时候,最理想的过弯路径是“外圈人弯,贴弯心出弯”.如图所示为赛车场的一个水平发卡弯,转弯处为圆心在O点的半圆,内外半径分别为r和2r,r=10m.一辆质量为m=800kg的赛车(含车手的质量)从A处进弯,从A′点出弯,过弯路线是以O′为圆心的半圆,OO′=r.赛车以不打滑的最大速率v=72km/h通过弯道(赛车速率不变),赛车能以此车速过弯是因为赛车形状都设计得使其上下方空气有一压力差-气动压力,从而增大了对地面的正压力.已知赛车轮胎与赛道附着系数η=0.8,附着系数可以看成是轮胎与路面的摩擦系数.这个系数越大,可利用的附着力(可视为静摩擦力)就越大,汽车就越不容易打滑,轮胎与赛道路面的滑动摩擦力与最大静摩擦力相等.求赛车沿此线路过弯时气动压力的最小值?
发卡弯是形容赛道上某个弯角程度的词,比较形象.发卡弯一般的角度都接近180°.赛车过这种弯道的时候,最理想的过弯路径是“外圈人弯,贴弯心出弯”.如图所示为赛车场的一个水平发卡弯,转弯处为圆心在O点的半圆,内外半径分别为r和2r,r=10m.一辆质量为m=800kg的赛车(含车手的质量)从A处进弯,从A′点出弯,过弯路线是以O′为圆心的半圆,OO′=r.赛车以不打滑的最大速率v=72km/h通过弯道(赛车速率不变),赛车能以此车速过弯是因为赛车形状都设计得使其上下方空气有一压力差-气动压力,从而增大了对地面的正压力.已知赛车轮胎与赛道附着系数η=0.8,附着系数可以看成是轮胎与路面的摩擦系数.这个系数越大,可利用的附着力(可视为静摩擦力)就越大,汽车就越不容易打滑,轮胎与赛道路面的滑动摩擦力与最大静摩擦力相等.求赛车沿此线路过弯时气动压力的最小值?