题目内容
小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑;坡道顶端距水平面高度为h,倾角为θ;物块从坡道进入水平滑道时,在底端O点处无机械能损失,重力加速度为g,将轻弹簧的一端连接在水平滑道M处并固定在墙上,另一自由端恰位于坡道的底端O点,如图所示.物块A从坡顶由静止滑下,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量时的弹性势能:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量时的弹性势能:

(1)对A到O的过程运用动能定理得,
mgh-μmgcosθ
=
mv2-0
所以v=
(2)弹簧压缩量最大时,速度为零,物块的动能全部转化为弹簧的弹性势能.根据能量守恒定律得,
Ep=
mv2=mgh-μmgcos
答:(1)物块滑到O点时的速度大小为v=
.
(2)弹簧为最大压缩量时的弹性势能为mgh-μmgcos
.
mgh-μmgcosθ
| h |
| sinθ |
| 1 |
| 2 |
所以v=
| 2gh-2μghcotθ |
(2)弹簧压缩量最大时,速度为零,物块的动能全部转化为弹簧的弹性势能.根据能量守恒定律得,
Ep=
| 1 |
| 2 |
| h |
| sinθ |
答:(1)物块滑到O点时的速度大小为v=
| 2gh-2μghcotθ |
(2)弹簧为最大压缩量时的弹性势能为mgh-μmgcos
| h |
| sinθ |

练习册系列答案
相关题目
 小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑;坡道顶端距水平面高度为h,倾角为θ;物块从坡道进入水平滑道时,在底端O点处无机械能损失,重力加速度为g.将轻弹簧的一端连接在水平滑道M处并固定墙上,另一自由端恰位于坡道的底端O点,如图所示.物块A从坡顶由静止滑下,求:
小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑;坡道顶端距水平面高度为h,倾角为θ;物块从坡道进入水平滑道时,在底端O点处无机械能损失,重力加速度为g.将轻弹簧的一端连接在水平滑道M处并固定墙上,另一自由端恰位于坡道的底端O点,如图所示.物块A从坡顶由静止滑下,求: 小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑;坡道顶端距水平面高度为h,倾角为θ;物块从坡道进入水平滑道时,在底端O点处无机械能损失,重力加速度为g,将轻弹簧的一端连接在水平滑道M处并固定在墙上,另一自由端恰位于坡道的底端O点,如图所示.物块A从坡顶由静止滑下,求:
小物块A的质量为m,物块与坡道间的动摩擦因数为μ,水平面光滑;坡道顶端距水平面高度为h,倾角为θ;物块从坡道进入水平滑道时,在底端O点处无机械能损失,重力加速度为g,将轻弹簧的一端连接在水平滑道M处并固定在墙上,另一自由端恰位于坡道的底端O点,如图所示.物块A从坡顶由静止滑下,求:
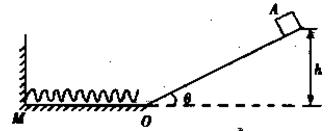
 如图所示.物块A从坡顶由静止滑下,求:
如图所示.物块A从坡顶由静止滑下,求: