��Ŀ����
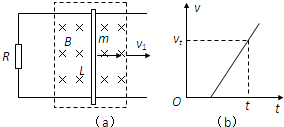
��ͼ��a����ʾ���⻬��ƽ�г�ֱ������������ˮƽ���ڣ����ΪL��������˽�����ֵΪR�ĵ��裬����Ϊm�ĵ������ֱ����ڵ����ϣ�����͵�����ĵ�������ƣ��ҽӴ����ã��ڵ���ƽ������һ���������ڴ�������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����ʼʱ���������ֹ�ڴų�������Ҷˣ����ų����ٶ�v1���������ƶ�ʱ���������֮��ʼ�˶���ͬʱ�ܵ�ˮƽ����СΪf�ĺ㶨���������ܿ�ﵽ�㶨�ٶȣ���ʱ������Դ��ڴų������ڣ�
��1����������ﵽ�ĺ㶨�ٶ�v2��
��2��Ϊʹ���������ų��˶�����������ܳ������٣�
��3��������Ժ㶨�ٶ��˶�ʱ����λʱ���ڿ˷����������Ĺ��͵�·�����ĵĵ繦�ʸ�Ϊ���
��4����t=0ʱ�ų��ɾ�ֹ��ʼˮƽ�������ȼ���ֱ���˶��������϶�ʱ������Ҳ���ȼ���ֱ���˶�����v-t��ϵ��ͼ��b����ʾ����֪��ʱ��t�����˲ʱ�ٶȴ�СΪvt����������ȼ���ֱ���˶�ʱ�ļ��ٶȴ�С��
��1����������ﵽ�ĺ㶨�ٶ�v2��
��2��Ϊʹ���������ų��˶�����������ܳ������٣�
��3��������Ժ㶨�ٶ��˶�ʱ����λʱ���ڿ˷����������Ĺ��͵�·�����ĵĵ繦�ʸ�Ϊ���
��4����t=0ʱ�ų��ɾ�ֹ��ʼˮƽ�������ȼ���ֱ���˶��������϶�ʱ������Ҳ���ȼ���ֱ���˶�����v-t��ϵ��ͼ��b����ʾ����֪��ʱ��t�����˲ʱ�ٶȴ�СΪvt����������ȼ���ֱ���˶�ʱ�ļ��ٶȴ�С��

��1���е�Ÿ�Ӧ���ɣ���
E=BL��v1-v2��
�պϵ�·ŷķ����
I=
��������ܰ�����
F=BIL=
�ٶȺ㶨ʱ��
=f
�ɵ�v2=v1-
��2��Ϊʹ���������ų��˶�����������ܳ������ܵ���������������������ʱ�����������Ϊ
fm=
��3�����������غ㣬��λʱ���ڿ˷����������Ĺ�����Ħ�����Ĺ���
P=FV=f(v1-
)
��·�����ĵĵ繦 P=
=
=
��4����
-f=ma�����Ҫ���ȼ����˶�������v1-v2Ϊ��������Ϊ��v����
a=
��
-f=ma
�ɽ��
a=
�𣺣�1����������ﵽ�ĺ㶨�ٶ�v2=v1-
��
��2��Ϊʹ���������ų��˶�����������ܳ���
��3��������Ժ㶨�ٶ��˶�ʱ����λʱ���ڿ˷����������Ĺ��͵�·�����ĵĵ繦�ʸ�Ϊf(v1-
)��
��4����������ȼ���ֱ���˶�ʱ�ļ��ٶȴ�СΪa=
��
E=BL��v1-v2��
�պϵ�·ŷķ����
I=
| E |
| R |
��������ܰ�����
F=BIL=
| B2L2(v1-v2) |
| R |
�ٶȺ㶨ʱ��
| B2L2(v1-v2) |
| R |
�ɵ�v2=v1-
| fR |
| B2L2 |
��2��Ϊʹ���������ų��˶�����������ܳ������ܵ���������������������ʱ�����������Ϊ
fm=
| B2L2v1 |
| R |
��3�����������غ㣬��λʱ���ڿ˷����������Ĺ�����Ħ�����Ĺ���
P=FV=f(v1-
| fR |
| B2L2 |
��·�����ĵĵ繦 P=
| E2 |
| R |
| B2L2(v1-v2)2 |
| R |
| f2R |
| B2L2 |
��4����
| B2L2(v1-v2) |
| R |
a=
| vt+��v |
| t |
��
| B2L2(at-v2) |
| R |
�ɽ��
a=
| B2L2vt+fR |
| B2L2t-mR |
�𣺣�1����������ﵽ�ĺ㶨�ٶ�v2=v1-
| fR |
| B2L2 |
��2��Ϊʹ���������ų��˶�����������ܳ���
| B2L2v1 |
| R |
��3��������Ժ㶨�ٶ��˶�ʱ����λʱ���ڿ˷����������Ĺ��͵�·�����ĵĵ繦�ʸ�Ϊf(v1-
| fR |
| B2L2 |
| f2R |
| B2L2 |
��4����������ȼ���ֱ���˶�ʱ�ļ��ٶȴ�СΪa=
| B2L2vt+fR |
| B2L2t-mR |

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ

 ��2007?�Ϻ�����ͼ��a����ʾ���⻬��ƽ�г�ֱ������������ˮƽ���ڣ����ΪL��������˽�����ֵΪR�ĵ��裬����Ϊm�ĵ������ֱ����ڵ����ϣ�����͵�����ĵ�������ƣ��ҽӴ����ã��ڵ���ƽ������һ���������ڴ�������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����ʼʱ���������ֹ�ڴų�������Ҷˣ����ų����ٶ�v1���������ƶ�ʱ���������֮��ʼ�˶���ͬʱ�ܵ�ˮƽ����СΪf�ĺ㶨���������ܿ�ﵽ�㶨�ٶȣ���ʱ������Դ��ڴų������ڣ�
��2007?�Ϻ�����ͼ��a����ʾ���⻬��ƽ�г�ֱ������������ˮƽ���ڣ����ΪL��������˽�����ֵΪR�ĵ��裬����Ϊm�ĵ������ֱ����ڵ����ϣ�����͵�����ĵ�������ƣ��ҽӴ����ã��ڵ���ƽ������һ���������ڴ�������ֱ���µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����ʼʱ���������ֹ�ڴų�������Ҷˣ����ų����ٶ�v1���������ƶ�ʱ���������֮��ʼ�˶���ͬʱ�ܵ�ˮƽ����СΪf�ĺ㶨���������ܿ�ﵽ�㶨�ٶȣ���ʱ������Դ��ڴų������ڣ� ��ͼ��a����ʾ���⻬ˮƽ����ͣ����һ���ϱ���ֲڵ�ƽ�峵������ΪM�������ϱ�������ĸ߶��복�ϱ��泤����ͬ��һ����Ϊm��������ˮƽ���ٶ�v0����С���ϣ����ǵ��ٶ���ʱ��仯��ͼ����ͼ��b����ʾ��t0�ǻ����ڳ����˶���ʱ�䣩���������ٶ�Ϊg���������ж���ȷ���ǣ�������
��ͼ��a����ʾ���⻬ˮƽ����ͣ����һ���ϱ���ֲڵ�ƽ�峵������ΪM�������ϱ�������ĸ߶��복�ϱ��泤����ͬ��һ����Ϊm��������ˮƽ���ٶ�v0����С���ϣ����ǵ��ٶ���ʱ��仯��ͼ����ͼ��b����ʾ��t0�ǻ����ڳ����˶���ʱ�䣩���������ٶ�Ϊg���������ж���ȷ���ǣ�������
