题目内容
10.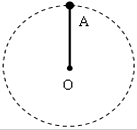 如图所示,长L=0.5m,质量可忽略的细绳,其一端固定在O点,上端连接着一个金属零件A,A的质量为1kg,它绕O点在竖直平面内做圆周运动,取重力加速度g=10m/s2.在零件A通过最高点时,求解下列问题:
如图所示,长L=0.5m,质量可忽略的细绳,其一端固定在O点,上端连接着一个金属零件A,A的质量为1kg,它绕O点在竖直平面内做圆周运动,取重力加速度g=10m/s2.在零件A通过最高点时,求解下列问题:(1)若此时细绳对零件A没有作用力,求零件A的速度大小;
(2)若此时零件A的速度大小为3m/s,求此时零件A对绳的作用力的大小和方向.
分析 (1)在最高点,细绳对零件A没有作用力,零件做圆周运动需要的向心力由重力提供,根据牛顿第二定律求解速度.
(2)在最高点,零件仅受重力与绳子的拉力,二力的合力提供向心力,列出牛顿第二定律方程解决.
解答 解:(1)对零件,根据牛顿第二定律得:mg=m$\frac{{v}_{A}^{2}}{L}$
可得 vA=$\sqrt{gL}$=$\sqrt{10×0.5}$=$\sqrt{5}$m/s
(1)当vA′=3m/s时,由牛顿第二定律得:mg+T=m$\frac{{v}_{A}^{′2}}{L}$
得 T=m($\frac{{v}_{A}^{′2}}{L}$-g)=1×($\frac{{3}^{2}}{0.5}$-10)N=8N
此时零件A对绳的作用力的大小为8N,方向向下.
答:
(1)零件A的速度大小为$\sqrt{5}$m/s;
(2)此时零件A对绳的作用力的大小为8N,方向向下.
点评 本题关键找出向心力来源,再根据向心力公式和牛顿第二定律联立列式求解!

练习册系列答案
相关题目
10.中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,是继美国全球定位系统(GPS),俄罗斯格洛纳斯卫星导航系统(GLONASS)之后第三个成熟的卫星导航系统.中国北斗卫星导航系统共由35颗卫星组成,其中2010年01月17日发射的卫星和2012年09月19日发射的卫星运行轨道分别为:高度为35807公里地球静止轨道卫星北斗-G1和高度为21576公里的中地球轨道卫星北斗-M6,下列说法正确的是( )
| A. | 北斗-G1的绕地运行周期大于北斗-M6的绕地运行周期 | |
| B. | 北斗-G1的绕地运行速率大于北斗-M6的绕地运行速率 | |
| C. | 北斗-G1的绕地运行的向心加速度大于北斗-M6的绕地运行向心加速度 | |
| D. | 北斗-G1只能在赤道的正上方 |
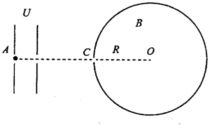 在光滑绝缘的水平面上,左侧平行极板间有水平方向匀强电场,右侧圆筒内有竖直方向匀强磁场,磁感应强度大小为B,俯视图如图所示,圆的圆心为O点,半径大小为R,一质量为m、电荷量大小为q的带电小球(可视为质点),初速位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,粒子和圆筒壁的碰撞没有动能和电荷量损失,B、R、m、q为已知量,圆筒仅有一个出入口C.
在光滑绝缘的水平面上,左侧平行极板间有水平方向匀强电场,右侧圆筒内有竖直方向匀强磁场,磁感应强度大小为B,俯视图如图所示,圆的圆心为O点,半径大小为R,一质量为m、电荷量大小为q的带电小球(可视为质点),初速位置在A点,现由静止经电场加速后从C孔沿直径射入磁场区域,粒子和圆筒壁的碰撞没有动能和电荷量损失,B、R、m、q为已知量,圆筒仅有一个出入口C. 如图所示,真空中存在空间范围足够大、方向水平向右的匀强磁场,在电场中,一个质量为m、电荷量为q的离子,以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动.
如图所示,真空中存在空间范围足够大、方向水平向右的匀强磁场,在电场中,一个质量为m、电荷量为q的离子,以大小为V0的初速度从O点以与电场负方向成θ=45°角的方向向上做直线运动.

 根据波尔原子结构理论,氦离子(He+)的能级图如图所示,当某个He+处在n=4的激发态时,由于跃迁所发射的谱线可能有几条( )
根据波尔原子结构理论,氦离子(He+)的能级图如图所示,当某个He+处在n=4的激发态时,由于跃迁所发射的谱线可能有几条( )