题目内容
11. 如图所示,质量mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量mA=2kg的物块A,一颗质量m0=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=200m/s.已知A与B之间的动摩擦因数μ=0.1,要使A最终不会从平板车B上落下,求平板车B的最小长度是多少?
如图所示,质量mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量mA=2kg的物块A,一颗质量m0=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=200m/s.已知A与B之间的动摩擦因数μ=0.1,要使A最终不会从平板车B上落下,求平板车B的最小长度是多少?
分析 子弹与A组成的系统动量守恒,由动量守恒定律可以求出A的速度;
A、B组成的系统动量守恒,由动量守恒定律可以求出B的速度,
然后应用能量守恒定律可以求出平板车的最小长度.
解答 解:对于子弹、物块A相互作用过程系统动力守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
m0v0=m0v+mAvB,
代入数据解得:vA=2m/s,
对于A、B相互作用作用过程系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得:
mAvA=(mA+mB)vB,
代入数据解得:vB=1m/s,
A、B系统因摩擦产生的热量等于A、B系统损失的动能,由能量守恒定律得:
μmgs=$\frac{1}{2}$mAvA2-$\frac{1}{2}$(mA+mB)vB2,
代入数据解得:s=1m;
答:平板车B的最小长度是1m.
点评 本题考查了动量守恒定律与能量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与能量守恒定律可以解题,难度不大.

练习册系列答案
相关题目
1.下列有关物理学史,不符合事实的是( )
| A. | 赫兹通过实验证实了电磁波的存在 | |
| B. | 牛顿发现了单摆周期公式 | |
| C. | 爱因斯坦的狭义相对论认为物体的质量与其运动状态有关 | |
| D. | 麦克斯韦建立了电磁场理论并预言了电磁波的存在 |
2.穿过同一闭合回路的磁通量Φ随时间t变化的图象分别如图中的①-④所示,下列关于回路中感应电动势的论述正确的是( )


| A. | 图①回路产生恒定不变的感应电动势 | |
| B. | 图②回路产生的感应电动势一直在变大 | |
| C. | 图③回路0~t1时间内产生的感应电动势小于t1~t2时间内产生的感应电动势 | |
| D. | 图④回路产生的感应电动势先变小再变大 |
19. 如图所示,轮A、B同轴转动,轮C、B间通过皮带传动,皮带不打滑.已知A、B、C三轮半径之比Ra:Rb:Rc:=3:1:2.由关于三轮边缘上三点a、b、c的线速度之比、角速度之比、向心加速度之比,正确的是( )
如图所示,轮A、B同轴转动,轮C、B间通过皮带传动,皮带不打滑.已知A、B、C三轮半径之比Ra:Rb:Rc:=3:1:2.由关于三轮边缘上三点a、b、c的线速度之比、角速度之比、向心加速度之比,正确的是( )
 如图所示,轮A、B同轴转动,轮C、B间通过皮带传动,皮带不打滑.已知A、B、C三轮半径之比Ra:Rb:Rc:=3:1:2.由关于三轮边缘上三点a、b、c的线速度之比、角速度之比、向心加速度之比,正确的是( )
如图所示,轮A、B同轴转动,轮C、B间通过皮带传动,皮带不打滑.已知A、B、C三轮半径之比Ra:Rb:Rc:=3:1:2.由关于三轮边缘上三点a、b、c的线速度之比、角速度之比、向心加速度之比,正确的是( )| A. | 1:1:3 2:2:1 1:2:6 | B. | 3:1:1 2:2:1 6:2:1 | ||
| C. | 1:3:1 2:2:1 2:6:1 | D. | 3:1:1 2:1:2 6:2:1 |
6. 如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN,重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )
如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN,重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )
 如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN,重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )
如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN,重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )| A. | $\frac{1}{2}$R(FN-2mg) | B. | $\frac{1}{2}$R(3mg-FN) | C. | $\frac{1}{2}$R(FN-mg) | D. | $\frac{1}{2}$R(FN-3mg) |
3.下列说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验建立了原子核式结构模型 | |
| B. | 宏观物体的物质波波长非常小,极难观察到它的波动性 | |
| C. | β衰变中产生的β射线实际上是原子核外电子挣脱原子核的束缚而形成的高速电子流 | |
| D. | 对于任何一种金属都存在一个“最小波长”,入射光的波长必须大于这个波长,才能产生光电效应 | |
| E. | 爱因斯坦在对光电效应的研究中,首先提出了光子说 |
1.某实验小组做探究弹力和弹簧伸长量的关系实验
(1)甲同学先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧的原长L0,再把弹簧竖直悬挂起来,挂上砝码后测出弹簧伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,由于弹簧自身重力的影响,最后画出的图线可能是图1的哪一个C.

(2)乙同学将弹簧和刻度尺竖直悬挂在铁架台上,待弹簧稳定时,记下长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
表中有一个数值记录不规范,代表符号为L3.
由表可知所用刻度尺的最小长度为1mm.
(3)图2是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与Lx的差值.由图可知弹簧的劲度系数为4.9N/m(结果保留两位有效数字,重力加速度取9.8m/s2).
(1)甲同学先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧的原长L0,再把弹簧竖直悬挂起来,挂上砝码后测出弹簧伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,由于弹簧自身重力的影响,最后画出的图线可能是图1的哪一个C.

(2)乙同学将弹簧和刻度尺竖直悬挂在铁架台上,待弹簧稳定时,记下长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如表:
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
由表可知所用刻度尺的最小长度为1mm.
(3)图2是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与Lx的差值.由图可知弹簧的劲度系数为4.9N/m(结果保留两位有效数字,重力加速度取9.8m/s2).

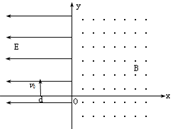 如图,在x<0的空间中,存在沿x轴负方向的匀强电场,电场强度E=10N/C;在x>0的空间中,存在垂直xy平面方向向外的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在距O点左边x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求
如图,在x<0的空间中,存在沿x轴负方向的匀强电场,电场强度E=10N/C;在x>0的空间中,存在垂直xy平面方向向外的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在距O点左边x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求