题目内容
5. 如图所示,在光滑的水平面上有一足够长的质量为m1的平板小车,正以速度v向右运动,现将以质量为m2的木块无初速度地放上小车,由于木块和小车间的摩擦力的作用,小车的速度将发生变化,为使小车保持原来的运动速度不变,必须及时对小车施加一向右的水平恒力,当该力作用一段时间后把它撤去时,木块恰能随小车一起以速度v共同向右运动,设木块和小车间的动摩擦因数为μ,求这个过程中:
如图所示,在光滑的水平面上有一足够长的质量为m1的平板小车,正以速度v向右运动,现将以质量为m2的木块无初速度地放上小车,由于木块和小车间的摩擦力的作用,小车的速度将发生变化,为使小车保持原来的运动速度不变,必须及时对小车施加一向右的水平恒力,当该力作用一段时间后把它撤去时,木块恰能随小车一起以速度v共同向右运动,设木块和小车间的动摩擦因数为μ,求这个过程中:(1)水平恒力对小车做了多少功?
(2)小车与木块间产生的热量.
分析 (1)对小车受力分析,根据平衡条件求解拉力F的大小;对木块受力分析,根据牛顿第二定律列式求解加速度,根据速度公式求解加速时间;最后根据功的定义求解拉力F的功;
(2)小车与木块间产生的热量Q=f•△S相对.
解答 解:(1)放上木块后,小车多受一个向左的滑动摩擦力,由于小车是匀速直线运动,根据平衡条件,有:
F=f=μm1g
放上木块后,木块加速度为:
a=-μg
达到速度v的时间为:
t=$\frac{v}{a}=\frac{v}{μg}$
故该时间内拉力的功为:
W=Fx1=μmg•(vt)=mv2
(2)木块位移为:
x=$\frac{1}{2}a{t}^{2}$=$\frac{{v}^{2}}{2μg}$
小车与木块的相对位移为:
$△x=vt-x=v•\frac{v}{μg}-\frac{{v}^{2}}{2μg}=\frac{{v}^{2}}{2μg}$
故摩擦产生的热量为:
Q=f•△x=$μmg•\frac{{v}^{2}}{2μg}$=$\frac{1}{2}m{v}^{2}$
答:(1)水平恒力对小车做的功为mv2;
(2)小车与木块间产生的热量为$\frac{1}{2}m{v}^{2}$.
点评 本题关键是要明确小车和木块的受力情况和运动情况,结合牛顿第二定律、动能定理和功能关系列式分析,不难.

练习册系列答案
相关题目
16. 某质点在一段时间内的位置-时间图象如图所示,关于0-t0时间内质点的运动情况,下列说法正确的是( )
某质点在一段时间内的位置-时间图象如图所示,关于0-t0时间内质点的运动情况,下列说法正确的是( )
 某质点在一段时间内的位置-时间图象如图所示,关于0-t0时间内质点的运动情况,下列说法正确的是( )
某质点在一段时间内的位置-时间图象如图所示,关于0-t0时间内质点的运动情况,下列说法正确的是( )| A. | 该质点做曲线运动 | B. | 该质点一直向+x方向运动 | ||
| C. | 该质点先加速后减速 | D. | 该质点可能做匀变速直线运动 |
13.子弹与速度v恰能击穿一块木板,设子弹所受阻力恒定,那么子弹的速度为3v时,能击穿相同的木块数为( )
| A. | 2块 | B. | 3块 | C. | 6块 | D. | 9块 |
20. 如图所示光滑T形架,水平部分套一质量为M的滑块,竖直部分套一质量为m的滑块,两滑块用轻绳相连,当T形架绕中轴线以角速度ω旋转时,轻绳与竖直方向夹角为θ,现减小T形架转速,下列说法正确的是( )
如图所示光滑T形架,水平部分套一质量为M的滑块,竖直部分套一质量为m的滑块,两滑块用轻绳相连,当T形架绕中轴线以角速度ω旋转时,轻绳与竖直方向夹角为θ,现减小T形架转速,下列说法正确的是( )
 如图所示光滑T形架,水平部分套一质量为M的滑块,竖直部分套一质量为m的滑块,两滑块用轻绳相连,当T形架绕中轴线以角速度ω旋转时,轻绳与竖直方向夹角为θ,现减小T形架转速,下列说法正确的是( )
如图所示光滑T形架,水平部分套一质量为M的滑块,竖直部分套一质量为m的滑块,两滑块用轻绳相连,当T形架绕中轴线以角速度ω旋转时,轻绳与竖直方向夹角为θ,现减小T形架转速,下列说法正确的是( )| A. | θ增大 | B. | 轻绳上拉力减小 | C. | M所受支持力增大 | D. | M所受合力减小 |
17. 在如图所示的甲、乙电路中,电阻R和灯泡电阻值相等,自感线圈L的电阻值可认为是零.在接通开关S时,则( )
在如图所示的甲、乙电路中,电阻R和灯泡电阻值相等,自感线圈L的电阻值可认为是零.在接通开关S时,则( )
 在如图所示的甲、乙电路中,电阻R和灯泡电阻值相等,自感线圈L的电阻值可认为是零.在接通开关S时,则( )
在如图所示的甲、乙电路中,电阻R和灯泡电阻值相等,自感线圈L的电阻值可认为是零.在接通开关S时,则( )| A. | 在电路甲中,A将渐渐变亮 | |
| B. | 在电路甲中,A将先变亮,后渐渐变暗 | |
| C. | 在电路乙中,A将渐渐变亮 | |
| D. | 在电路乙中,A将由亮渐渐变暗,后熄灭 |
14. 图中圆弧轨道AB是在竖直平面内的$\frac{1}{4}$圆周,在B点,轨道的切线是水平的.一质点自A点从静止开始下滑,不计滑块与轨道间的摩擦和空气阻力,则在质点刚要到达B点时的加速度大小和刚滑过B点时的加速度大小分别为( )
图中圆弧轨道AB是在竖直平面内的$\frac{1}{4}$圆周,在B点,轨道的切线是水平的.一质点自A点从静止开始下滑,不计滑块与轨道间的摩擦和空气阻力,则在质点刚要到达B点时的加速度大小和刚滑过B点时的加速度大小分别为( )
 图中圆弧轨道AB是在竖直平面内的$\frac{1}{4}$圆周,在B点,轨道的切线是水平的.一质点自A点从静止开始下滑,不计滑块与轨道间的摩擦和空气阻力,则在质点刚要到达B点时的加速度大小和刚滑过B点时的加速度大小分别为( )
图中圆弧轨道AB是在竖直平面内的$\frac{1}{4}$圆周,在B点,轨道的切线是水平的.一质点自A点从静止开始下滑,不计滑块与轨道间的摩擦和空气阻力,则在质点刚要到达B点时的加速度大小和刚滑过B点时的加速度大小分别为( )| A. | 0,g | B. | g,g | C. | 2g,g | D. | 2g,2g |
15.如图所示,某物体沿$\frac{1}{4}$光滑圆弧轨道由最高点滑到最低点过程中,下列说法正确的是( )


| A. | 物体做匀速圆周运动 | |
| B. | 物体所受的合力方向始终指向圆心O | |
| C. | 物体所受的支持力大小不变 | |
| D. | 物体所受的合力做正功 |
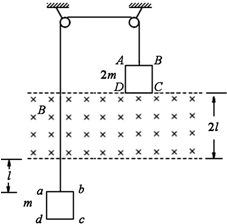 如图所示,竖直面内的正方形导线框ABCD和abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l,现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求:
如图所示,竖直面内的正方形导线框ABCD和abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l,现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求: