题目内容
 如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg.当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1m.竖直轴AB匀速转动,C球在水平面内做匀速圆周运动.求:
如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为2mg.当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1m.竖直轴AB匀速转动,C球在水平面内做匀速圆周运动.求:(1)要使两条细绳都拉直,C球的线速度至少多大?
(2)当C球的线速度增大时,AC和BC哪条绳先断?当其中一条绳刚要断时,C球的线速度多大?(g=10m/s2,sin53°=0.8,cos53°=0.6)
分析:(1)当小球线速度增大时,BC逐渐被拉直,小球线速度增至BC刚被拉直时,对小球进行受力分析,合外力提供向心力,根据向心力公式求出C球速度;
(2)当绳子拉直时,线速度再增大时,TA不变,而TB增大,所以BC绳先断,当TB=2mg时,绳子断裂,根据向心力公式求出此时C的速度;
(2)当绳子拉直时,线速度再增大时,TA不变,而TB增大,所以BC绳先断,当TB=2mg时,绳子断裂,根据向心力公式求出此时C的速度;
解答:解:(1)当小球线速度增大时,BC逐渐被拉直,小球线速度增至BC刚被拉直时,
对球:TAsin∠ACB-mg=0…①
TAcos∠ACB=m
…②
由①②解得:v=
m/s
(2)当绳子拉直时,线速度再增大时,①仍然成立,TA不变,而TB增大,所以BC绳先断,当TB=2mg时,
根据向心力公式得:
2mg+TAcos∠ACB=m
③
由①③解得:v′=
m/s
答:(1)要使两条细绳都拉直,C球的线速度至少为
m/s;(2)当C球的线速度增大时,BC绳先断,当其中一条绳刚要断时,C球的线速度为
m/s.
对球:TAsin∠ACB-mg=0…①
TAcos∠ACB=m
| v2 |
| BC |
由①②解得:v=
| ||
| 2 |
(2)当绳子拉直时,线速度再增大时,①仍然成立,TA不变,而TB增大,所以BC绳先断,当TB=2mg时,
根据向心力公式得:
2mg+TAcos∠ACB=m
| v′2 |
| BC |
由①③解得:v′=
| ||
| 2 |
答:(1)要使两条细绳都拉直,C球的线速度至少为
| ||
| 2 |
| ||
| 2 |
点评:解决本题的关键搞清向心力的来源,运用牛顿第二定律进行求解,难度适中.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为 2mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1m,ABC能绕竖直轴AB匀速转动,而C球在水平面内做匀速圆周运动,求:
如图所示,AB为竖直转轴,细绳AC和BC的结点C系一质量为m的小球,两绳能承担的最大拉力均为 2mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1m,ABC能绕竖直轴AB匀速转动,而C球在水平面内做匀速圆周运动,求: 如图所示,AB为竖直直径,AC弦为光滑斜面轨道,为了测量滑块从A点由静止释放滑至C点的时间,只需测量的物理量是( )
如图所示,AB为竖直直径,AC弦为光滑斜面轨道,为了测量滑块从A点由静止释放滑至C点的时间,只需测量的物理量是( ) (2008?盐城二模)如图所示,AB为竖直墙壁,A点和P点在同一水平面上.空间存在着竖直方向的匀强电场.将一带电小球从P点以速度v向A抛出,结果打在墙上的C处.若撤去电场,将小球从P点以初速
(2008?盐城二模)如图所示,AB为竖直墙壁,A点和P点在同一水平面上.空间存在着竖直方向的匀强电场.将一带电小球从P点以速度v向A抛出,结果打在墙上的C处.若撤去电场,将小球从P点以初速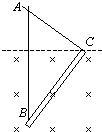 如图所示,AB为竖直固定金属棒,金属杆BC重为G.长为L,并可绕过B点垂直纸面的水平轴无摩擦转动,AC为轻质金属线,∠ABC=37°,∠ACB=90°,在图示范围内有一匀强磁场,其磁感应强度与时间成正比:B=k t,整个回路总电阻为R,则回路中感应电流I=
如图所示,AB为竖直固定金属棒,金属杆BC重为G.长为L,并可绕过B点垂直纸面的水平轴无摩擦转动,AC为轻质金属线,∠ABC=37°,∠ACB=90°,在图示范围内有一匀强磁场,其磁感应强度与时间成正比:B=k t,整个回路总电阻为R,则回路中感应电流I=