题目内容

两个半径为R的圆形平板电极，平行正对放置，相距为d，极板间的电势差为U，板间电场可以认为是均匀的．一个a粒子从正极板边缘以某一初速度垂直于电场方向射入两极板间，到达负极板时恰好落在极板中心．已知质子带电荷量为e，质子和中子的质量均为m，忽略重力和空气阻力的影响，则（　　）
分析：因为极板间是匀强电场，电场强度直接可根据匀强电场公式求出．质子进入电场后做类平抛运动，在沿电场方向上做初速度为零的匀加速直线运动，在垂直于电场方向上做匀速直线运动．α粒子在极板间运动的加速度a可以根据所受的合力（电场力）求出，α粒子的初速度v0可以根据两分运动的等时性去求解．
解答：解：A、极间场强E=
U
d
，故极板间的电场强度E=
U
d
，故A正确；
B、α粒子在极板间运动的加速度a=
qE
m
，代入得：a=
eU
2md
，故B正确；
C、由d=
1
2
at2得：t=
2d
a
=2d
e
mU
，故v0=
R
t
=
R
2d
eU
m
，故C错误；
D、初动能为：Ek0=
1
2
m
v
2
0
=
R2eU
8m2d2
，故D错误；
故选AB．
点评：解决本题关键会对类平抛运动进行分解，注意两分运动的等时性．
练习册系列答案
相关题目
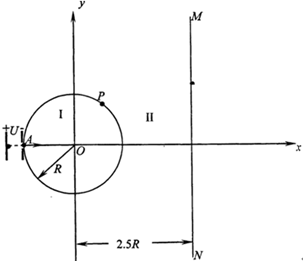精英家教网如图所示，在平面直角坐标系xOy平面内存在着方向相反的两个匀强磁场区域，其中圆心在坐标原点、半径为R的圆形区域Ⅰ内磁场方向垂直于xOy平面向里，第一象限和第四象限的圆形区域外（区域Ⅱ）的磁场方向垂直于xOy平面向外，MN为与x轴垂直且与y轴相距2.5R的一条直线，现有一质量为m、电荷量为+q的带电粒子，经过加速电压为U的加速电场加速后，从坐标为（-R，0）的A点沿x轴正方向射入区域Ⅰ，并从横坐标为0.5R处的P点进入区域Ⅱ．已知粒子第一次经过直线MN和第二次经过直线MN时的速度方向恰好相反，不计粒子重力，求：
（1）粒子进入圆形区域Ⅰ时的运动速度v的大小；
（2）区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小；
（3）粒子从A点开始到第二次经过直线MN的过程中运动的总时间t．

如图1所示，有一半径r的圆形有界匀强磁场B垂直纸面向里，其周围对称放置带有中心孔a，b，c的三个相同的平行板电容器，三个电容器两板间距离均为d，接有相同的电压U，在D处有一静止的电子，质量为m，电量为e，释放后从a孔射入匀强磁场中，并先后穿过b，c孔再从a孔穿出回到D处，求：

(1)匀强磁场的磁感应强度B的大小；

(2)电子从D出发到第一次回到D处所用的时间．

如图半径为R的圆形导体线圈，两端MN接一个平行板电容器，线圈垂直放在随时间均匀变化的匀强磁场中，要使电容器所带电量Q增大，可采取的措施是：

A．改变线圈所在的平面与磁场方向夹角

B．电容器两个极板再靠近些

C．增大磁感应强度的变化率

D．增大线圈的半径R

（12分）如图所示，在平面直角坐标系xOy平面内存在着方向相反的两个匀强磁场区域，其中圆心在坐标原点、半径为R的圆形区域Ⅰ内磁场方向垂直于xOy平面向里，第一象限和第四象限的圆形区域外（区域Ⅱ）的磁场方向垂直于xOy平面向外，MN为与x轴垂直且与y轴相距2.5R的一条直线，现有一质量为m、电荷量为+q的带电粒子，经过加速电压为U的加速电场加速后，从坐标为(－R，0)的A点沿x轴正方向射入区域Ⅰ，并从横坐标为0.5R处的P点进入区域Ⅱ．已知粒子第一次经过直线MN和第二次经过直线MN时的速度方向恰好相反，不计粒子重力，求：

（1）粒子进入圆形区域Ⅰ时的运动速度v的大小；       

（2）区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小；

（3）粒子从A点开始到第二次经过直线MN的过程中运动的总时间t.

 

如图所示，竖直平面内的轨道由一半径为4R、圆心角为的圆形的光滑滑槽C1和两个半径为R的半圆形光滑滑槽C2、C3以及一个半径为2R的半圆形光滑圆管C4组成，C4内径远小于R。C1、C2、C3、C4各衔接处平滑连接。现有一个比C4内径略小的、质量为m的小球，从与C4的最高点H等高的P点以一定的初速度向左水平抛出后，恰好沿C1的A端点沿切线从凹面进入轨道。已知重力加速度为g。求：

（1）小球在P点开始平抛的初速度的大小；

（2）小球能否依次顺利通过C1、C2、C3、C4各轨道而从I点射出？请说明理由；

（3）小球运动到何处，轨道对小球的弹力最大？最大值是多大？

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网