��Ŀ����
15��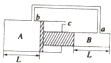 ��ͼ����T���λ��������������ڵ�����ָ���A��B�����֣����������������֮��ΪS1��S2=2��1���������������˵ײ������ΪL=10cm����������a��b��c����С���������ͨ���ֽ�a��b��ϸ�ܣ��ݻ����ƣ����ӣ���֪����ѹǿΪ��0=1.0��105Pa�������¶�ΪT0=300K��������ױڼ���Ħ���Ҳ�©����
��ͼ����T���λ��������������ڵ�����ָ���A��B�����֣����������������֮��ΪS1��S2=2��1���������������˵ײ������ΪL=10cm����������a��b��c����С���������ͨ���ֽ�a��b��ϸ�ܣ��ݻ����ƣ����ӣ���֪����ѹǿΪ��0=1.0��105Pa�������¶�ΪT0=300K��������ױڼ���Ħ���Ҳ�©���������������̶���Ȼ�������建�����ȵ�T1=360K�����ʱ���������ѹǿ��
�����������������ƶ����ı���������¶ȣ����ֻ������һ����ƶ��ˡ�L=2cm�������ƶ������в��ᾭ��С�ף��������¶�Ϊ���٣�
���� ��1�����ö��ӽ������̶���Ȼ�������建�����ȵ�T1����ʱ�������������ݱ仯���ɲ������ɼ������ĩ״̬��ѹǿ��
��2���������¶���ΪT0���ε����ӣ�Ȼ��ı���������¶ȣ����ڻ���������С���䣬���������ѹǿ���䣬�ɸ�•�����˶��ɼ������ĩ״̬���¶ȣ�
��� �⣺��1��A��B������ͨ����״̬ѹǿΪP0�����ڶ��ӽ������̶��������������
�ɲ������ɿ�֪��$\frac{{P}_{0}}{{T}_{0}}=\frac{{P}_{1}}{{T}_{1}}$
���� ${P}_{1}=\frac{{P}_{0}{T}_{1}}{{T}_{0}}$
�������ݵã�${P}_{1}=1.2��1{0}^{5}$Pa
��2���Ի�������������������֪�¶ȸı����������С���䣬���Ի��������ƶ��������ѹǿ���䣮���������ƶ��������������
�� $\frac{{V}_{1}}{{T}_{1}}=\frac{{V}_{2}}{{T}_{2}}$��֪����ʱ�¶����ߣ�
$\frac{{��{S_1}+{S_2}��L}}{T_0}=\frac{{{S_2}��L-��L��+{S_1}��L+��L��}}{T}$
��ã�$T={T_0}+\frac{{��{S_1}-{S_2}����L}}{{��{S_1}+{S_2}��L}}{T_0}$
�������ݵã�T=320K
�𣺣�1�����ö��ӽ������̶���Ȼ�������建�����ȵ�360K����ʱ���������ѹǿ��1.2��105Pa��
��2��������¶�Ϊ320K��
���� ���⿼�����������״̬���̵�Ӧ�ã������ؼ��Ի�������������õ���������ǵ�ѹ�仯��Ȼ�����״̬�����з�����⣬���ѣ�

 ��У����ϵ�д�
��У����ϵ�д� ��ͼ��ʾ������ֱƽ������һ�뾶ΪR��Բ��������뾶OAˮƽ��OB��ֱ��һ������Ϊm��С����Ϊ�ʵ㣩��A�����Ϸ�P���ɾ�ֹ��ʼ�������䣬С���ع��������ߵ�Bʱǡ�öԹ��û��ѹ������֪AP=2R���������ٶ�Ϊg����С���P��B���˶������У�������
��ͼ��ʾ������ֱƽ������һ�뾶ΪR��Բ��������뾶OAˮƽ��OB��ֱ��һ������Ϊm��С����Ϊ�ʵ㣩��A�����Ϸ�P���ɾ�ֹ��ʼ�������䣬С���ع��������ߵ�Bʱǡ�öԹ��û��ѹ������֪AP=2R���������ٶ�Ϊg����С���P��B���˶������У�������| A�� | ��������2mgR | B�� | ��е�ܼ���mgR | ||
| C�� | ��������mgR | D�� | �˷�Ħ��������$\frac{1}{2}$mgR |
| A�� | $\frac{1}{2}$T | B�� | T | C�� | $\sqrt{2}$T | D�� | $\frac{\sqrt{2}}{2}$T |
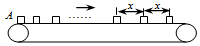 ��һˮƽ���������˶��Ĵ��ʹ������A�㣬ÿ��ʱ��T�����һ����ͬ�Ĺ�������֪�����봫�ʹ��䶯Ħ������Ϊ�̣�����������Ϊm����������������Щ�Ѿ��ʹ��ʹ��ﵽ��ͬ�ٶȵĹ���֮��ľ���Ϊx�������ж�һ����ȷ���ǣ�������
��һˮƽ���������˶��Ĵ��ʹ������A�㣬ÿ��ʱ��T�����һ����ͬ�Ĺ�������֪�����봫�ʹ��䶯Ħ������Ϊ�̣�����������Ϊm����������������Щ�Ѿ��ʹ��ʹ��ﵽ��ͬ�ٶȵĹ���֮��ľ���Ϊx�������ж�һ����ȷ���ǣ�������| A�� | ���ʹ����ٶ�Ϊ$\frac{x}{T}$ | |
| B�� | ���ʹ����ٶ�Ϊ2$\sqrt{2��gx}$ | |
| C�� | ÿ�������봫�ʹ�����Ħ��������������Ϊ$\frac{1}{2}$��mgx | |
| D�� | ��һ���൱����ʱ��t�ڣ����ʹ���Ϊ�������������ĵ�����Ϊ$\frac{mt{x}^{2}}{{T}^{2}}$ |
 ��ͼ��ʾ��ͼ����������ǿ�糡�У����Ǹպ���һ���뾶ΪR=0.2m��Բ���ĸ��ȷֵ��Բ��O��b��c��d����ĵ�����ͼ����֪�糡����Բ����ƽ��ƽ�У����ڵȷֵ�a����Բ��O���ĵ��Ƽ��糡ǿ�ȣ�����������ȷ���ǣ�������
��ͼ��ʾ��ͼ����������ǿ�糡�У����Ǹպ���һ���뾶ΪR=0.2m��Բ���ĸ��ȷֵ��Բ��O��b��c��d����ĵ�����ͼ����֪�糡����Բ����ƽ��ƽ�У����ڵȷֵ�a����Բ��O���ĵ��Ƽ��糡ǿ�ȣ�����������ȷ���ǣ�������| A�� | a��ĵ���Ϊ4V | B�� | O��ĵ���Ϊ5V | ||
| C�� | �糡ǿ�ȷ�����O��ָ��b�� | D�� | �糡ǿ�ȵĴ�СΪ10$\sqrt{5}$v/m |
| A�� | ������ | B�� | ţ�� | C�� | ���ĵ��� | D�� | ����˹̹ |
 ��ͼʾ������ʽ�������ͨ����ֵΪ100������ʱ����5�������ڲ���������Ϊ40J���˽��������Ƶ��Ϊ50Hz��������Ϊ2$\sqrt{2}$A��
��ͼʾ������ʽ�������ͨ����ֵΪ100������ʱ����5�������ڲ���������Ϊ40J���˽��������Ƶ��Ϊ50Hz��������Ϊ2$\sqrt{2}$A�� һ�⾵�Ľ���Ϊֱ��������ABC����A=30�㣬б��AB=a���⾵���ϵ�������Ϊn=$\sqrt{2}$���ڴ˽������ڵ�ƽ���ڣ�һ��������45�������Ǵ�AC�ߵ��е�M�����⾵�����ߴ��⾵���ʱ��������λ�ã������ǹ�����ԭ��·���ص��������
һ�⾵�Ľ���Ϊֱ��������ABC����A=30�㣬б��AB=a���⾵���ϵ�������Ϊn=$\sqrt{2}$���ڴ˽������ڵ�ƽ���ڣ�һ��������45�������Ǵ�AC�ߵ��е�M�����⾵�����ߴ��⾵���ʱ��������λ�ã������ǹ�����ԭ��·���ص��������