题目内容
13.在远距离输电时,要考虑尽量减少输电线上的功率损失,有一个小型发电站,输送的电功率为P=500kW,当使用U=5kV的电压输电时,测得安装在输电线路起点和终点处的两只电能表每小时示数相差200kW•h.求(1)输电效率η.
(2)输电线的总电阻R.
(3)若想使输电效率提高到98.4%,又不改变输电线路,那么发电站应采用多高的电压向外输电?
分析 (1)由起点与终点两只电表的示数相差,可求出输电效率.
(2)由损失的功率及相差的电压从而能求出线路上的电流,进而算出线路上的电阻.
(3)根据损失的功率求出输送电流的大小,结合P=UI求出输送的电压.
解答 解:(1)输送功率为:P=500kW,一小时输送电能为:E=Pt=500kW•h
输电线上损失的电能为:△E=200kW•h
终点得到的电能为:E′=E-△E=300kW•h
所以输电效率为:η=$\frac{E′}{E}$×100%=60%
(2)输电线上的电流为:I=$\frac{P}{U}$=$\frac{5×1{0}^{5}}{5×1{0}^{3}}$=100A
输电线损耗功率为:△P=I2R=200kW,
得:R=20Ω.
(3)当η=98.4%,△P=8kW,
因△P=I2R,则I=20A
输电电压为:U′=$\frac{P}{I}$=$\frac{5×1{0}^{5}}{20}$V=25000V=25kV
答:(1)输电效率η是60%.
(2)输电线的总电阻R是20Ω.
(3)发电站应采用25kV的电压向外输电.
点评 解决本题的关键知道输送功率、输送电压、电流之间的关系,掌握输电线上损失的功率公式△P=I2R.

练习册系列答案
相关题目
3.某人把原来静止于地面上的质量为2.0kg的物体向上提起1.0m,并使物体获得1.0m/s的速度,取g为10m/s2,则在此过程中( )
| A. | 重力对物体做功20J | B. | 人对物体做功20J | ||
| C. | 物体的机械能增加1.0J | D. | 合外力对物体做功1.0J |
4.理论和实践证明,开普勒定律不仅适用于太阳系中的天体运动,而且对一切天体(包括卫星绕行星的运动)都适用.对于开普勒第三定律的公式$\frac{{R}^{3}}{{T}^{2}}$=K,下列说法正确的是( )
| A. | 公式只适用于轨道是椭圆的运动 | |
| B. | 公式中的T为天体的自转周期 | |
| C. | 公式中的k值,只与中心天体有关,与绕中心天体公转的行星(或卫星)无关 | |
| D. | 若已知月球与地球之间的距离,根据开普勒第三定律公式可求出地球与太阳之间的距离 |
1.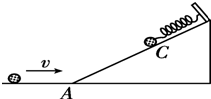 如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )
 如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )
如图所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为V,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则从A到C的过程中弹簧弹性势能的增加量是( )| A. | mgh-$\frac{1}{2}$mv2 | B. | $\frac{1}{2}$mv2-mgh | C. | -mgh | D. | -[mgh+$\frac{1}{2}$mv2] |
8. 如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )
如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )
 如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )
如图所示,一轻质弹簧一端固定,另一端与物体A相连接并使A在光滑水平面上做简谐运动,当A到达最大位移处时,把物块B由静止放置在A上面,此后A、B保持相对静止,共同做简谐运动,下列说法正确的是( )| A. | 振幅将比原来小 | |
| B. | 经过平衡位置的速度大小和原来相等 | |
| C. | 振子由最大位移处回到平衡位置所用时间和原来相同 | |
| D. | A对B的静摩擦力大小与弹簧形变量成正比 |
18. 如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )
如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )
 如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )
如图所示,A、B、C是在地球大气层外圆形轨道上运动的3颗卫星,已知mA=mB>mC,下列说法正确的是( )| A. | 角速度大小的关系是ωA>ωB=ωC | B. | 周期关系是TA>TB=TC | ||
| C. | 向心力大小的关系是FA=FB>FC | D. | 向心加速度大小的关系是aA<aB=aC |
3.氧气钢瓶充气后压强高于外界大气压,因某种原因,钢瓶缓慢漏气,假设缓慢漏气过程中瓶内外温度始终相等且保持不变,忽略氧气分子之间的相互作用.在漏气过程中,关于瓶内氧气的下列说法正确的是( )
| A. | 分子总数减少,分子总动能不变 | B. | 密度降低,分子平均动能不变 | ||
| C. | 吸收热量,对外做功 | D. | 压强降低,不对外做功 |
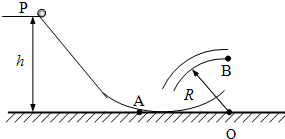 如图所示,轨道由斜直轨道、凹形圆弧轨道和半径R=2.0m的圆弧管道(内径不计)组成,三部分轨道均光滑处于同一竖直平面内,且依次平滑连接,A 点为凹形圆弧轨道的最低点,B点为圆弧管道的最高点,圆弧管道的圆心O点与A点处在同一水平面上.一质量m=0.10kg、可视为质点的小球从斜直轨道上的P点无初速滑下,经过A点向B点运动,P点距A点所在水平面的高度h=2.5m,不计一切阻力,g=9.8m/s2.
如图所示,轨道由斜直轨道、凹形圆弧轨道和半径R=2.0m的圆弧管道(内径不计)组成,三部分轨道均光滑处于同一竖直平面内,且依次平滑连接,A 点为凹形圆弧轨道的最低点,B点为圆弧管道的最高点,圆弧管道的圆心O点与A点处在同一水平面上.一质量m=0.10kg、可视为质点的小球从斜直轨道上的P点无初速滑下,经过A点向B点运动,P点距A点所在水平面的高度h=2.5m,不计一切阻力,g=9.8m/s2.