题目内容
20.我国研制的某种火箭,从静止开始竖直向上发射时的质量是2.4×l05kg,推力为3.0×l06N,则开始发射时的加速度是2.5m/s2.升空后随着燃料的消耗,如果推力维持不变,则它的加速度将变大(选填“变小”、“变大”或“不变”).分析 竖直发射时,火箭受推力和重力,根据牛顿第二定律可以求加速度;升空后消耗燃料,根据牛顿第二定律得到加速度表达式再讨论.
解答 解:对火箭受力分析,根据牛顿第二定律:F-mg=ma
解得:$a=\frac{F-mg}{m}=\frac{3.0×1{0}_{\;}^{6}-2.4×1{0}_{\;}^{6}}{2.4×1{0}_{\;}^{5}}=2.5m/{s}_{\;}^{2}$
升空后燃料消耗,F-mg=ma
$a=\frac{F}{m}-g$,推力不变,质量变小,加速度将变大;
故答案为:2.5,变大
点评 本题关键是根据火箭的运动情况得到加速度,关键是注意上升过程中,消耗燃料质量减小.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
10. 如图所示,人造地球卫星在万有引力作用下,做以地心为焦点的椭圆运动;MPN为椭圆上的三点,P是近地点;卫星在从M经P到达N点的过程中( )
如图所示,人造地球卫星在万有引力作用下,做以地心为焦点的椭圆运动;MPN为椭圆上的三点,P是近地点;卫星在从M经P到达N点的过程中( )
 如图所示,人造地球卫星在万有引力作用下,做以地心为焦点的椭圆运动;MPN为椭圆上的三点,P是近地点;卫星在从M经P到达N点的过程中( )
如图所示,人造地球卫星在万有引力作用下,做以地心为焦点的椭圆运动;MPN为椭圆上的三点,P是近地点;卫星在从M经P到达N点的过程中( )| A. | 动能先增大后减小 | B. | 势能先增大后减小 | ||
| C. | 加速度先增大后减小 | D. | 受到的向心力先减小后增加 |
10.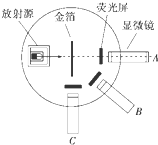 如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
 如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )| A. | 相同时间内放在A位置时观察到屏上的闪光次数最少 | |
| B. | 相同时间内放在B位置时观察到屏上的闪光次数最少 | |
| C. | 相同时间内放在C位置时观察到屏上的闪光次数最少 | |
| D. | 放在C位置时观察不到屏上有闪光 |
 如图甲所示,加有高压的阴极射线管可以显示高速电子束的径迹.不加磁场时,电子束是一条直线,加上如图乙所示的磁场后,电子束明显发生了偏转,电子束发生偏转是因为运动的电子受到了洛伦兹力.电子束在磁场中发生偏转在技术上有许多应用,例如:电视机显像管(举一应用实例).
如图甲所示,加有高压的阴极射线管可以显示高速电子束的径迹.不加磁场时,电子束是一条直线,加上如图乙所示的磁场后,电子束明显发生了偏转,电子束发生偏转是因为运动的电子受到了洛伦兹力.电子束在磁场中发生偏转在技术上有许多应用,例如:电视机显像管(举一应用实例).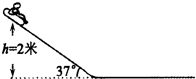 如图所示,一滑雪场有一倾角为37°的雪坡,雪坡上的雪道与水平雪道相连.一个人坐在玩具雪橇里从雪坡上高2m处由静止开始自由滑下,雪橇与雪道的动摩擦因数为0.075.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
如图所示,一滑雪场有一倾角为37°的雪坡,雪坡上的雪道与水平雪道相连.一个人坐在玩具雪橇里从雪坡上高2m处由静止开始自由滑下,雪橇与雪道的动摩擦因数为0.075.(g=10m/s2,sin37°=0.6,cos37°=0.8)求: 如图是探究电磁感应现象的实验装置,请写出能产生感应电流的两种操作方法:
如图是探究电磁感应现象的实验装置,请写出能产生感应电流的两种操作方法: 如图所示,在铁芯P上绕着两个线圈甲和乙,如果线圈甲中电流i与时间t的关系有图中A、B、C、D 4种情况,在t1~t2这段时间内,哪种情况在线圈乙中会产生变化的感应电流( )
如图所示,在铁芯P上绕着两个线圈甲和乙,如果线圈甲中电流i与时间t的关系有图中A、B、C、D 4种情况,在t1~t2这段时间内,哪种情况在线圈乙中会产生变化的感应电流( )







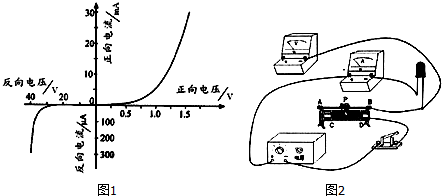
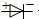 ”,且具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻比较大.厂家提供的伏安特性曲线如图1.某兴趣小组测绘施加反向电压时的伏安特性曲线,以验证与厂家提供的数据是否一致,可选用的器材有:
”,且具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻比较大.厂家提供的伏安特性曲线如图1.某兴趣小组测绘施加反向电压时的伏安特性曲线,以验证与厂家提供的数据是否一致,可选用的器材有: