题目内容
15. 如图所示,将小球a从地面以某一初速度竖直上抛的同时,将另一相同质量的小球b从距地面h处由静止释放,两球恰在$\frac{h}{2}$处相遇(不计空气阻力,重力加速度为g),问:
如图所示,将小球a从地面以某一初速度竖直上抛的同时,将另一相同质量的小球b从距地面h处由静止释放,两球恰在$\frac{h}{2}$处相遇(不计空气阻力,重力加速度为g),问:(1)两个小球落地的时间差△t;
(2)若小球a的初速度增大到原来$\sqrt{2}$倍,问a球上升过程中与b球相遇的位置距离地面多高?
分析 (1)根据题意分析可知,ab两个球在相等的时间内,运动距离都是$\frac{h}{2}$,加速度大小也相等,所以说明在该过程处相遇时a球的速度刚好为0,而b球的速度刚好为v0;
(2)对两球分析,根据相遇问题的条件进行列式即可求得相遇时间,由位移公式即可得相遇位置.
解答 解:(1)对b球由自由落体规律可知,$\frac{h}{2}$=$\frac{1}{2}$gt2;
对a球可知,$\frac{h}{2}$=v0t-$\frac{1}{2}$gt2;
解得:v0t=h
则可知,$\frac{{v}_{0}t}{2}$=$\frac{h}{2}$;
故说明小球a到达最高点的速度为0;
两球下落的是间差相当于a球从中间位置自由下落,b球从中间位置以一定初速度匀加速下落;
a下落时间ta=$\sqrt{\frac{h}{g}}$;
b下落时间为:tb=$\sqrt{\frac{2h}{g}}$-$\sqrt{\frac{h}{g}}$;
故时间差为:△t=ta-tb=2$\sqrt{\frac{h}{g}}$-$\sqrt{\frac{2h}{g}}$;
(2)由(1)的分析可知,a的初速度v0=$\sqrt{gh}$;
以$\sqrt{2}$v0上抛时;设经时间为t;
则a的位移xa=($\sqrt{2gh}$)t-$\frac{1}{2}$gt2;
b的位移xb=$\frac{1}{2}$gt2;
xa+xb=h;
则有:$\sqrt{2gh}$t=h
解得:t=$\sqrt{\frac{h}{2g}}$
b下落高度xb=$\frac{1}{2}g×\sqrt{\frac{h}{2g}}$=$\frac{\sqrt{2gh}}{4}$
距地面高度为h-$\frac{\sqrt{2gh}}{4}$;
答:(1)两个小球落地的时间差△t为2$\sqrt{\frac{h}{g}}$-$\sqrt{\frac{2h}{g}}$;
(2)若小球a的初速度增大到原来$\sqrt{2}$倍,问a球上升过程中与b球相遇的位置距离地面h-$\frac{\sqrt{2gh}}{4}$;
点评 根据题目的介绍分析得出ab球的运动之间的关系是解答本题的关键,这要求熟练的掌握自由落体和竖直上抛运动的规律

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案 如图所示,图中以点电荷Q为圆心的虚线同心圆是该点电荷电场中球形等势面的横截面图.一个带正电的粒子经过该电场,它的运动轨迹如图中实线所示,M和N是轨迹上的两点.不计带电粒子受到的重力,由此可以判断( )
如图所示,图中以点电荷Q为圆心的虚线同心圆是该点电荷电场中球形等势面的横截面图.一个带正电的粒子经过该电场,它的运动轨迹如图中实线所示,M和N是轨迹上的两点.不计带电粒子受到的重力,由此可以判断( )| A. | 此粒子在M点的加速度大于在N点的加速度 | |
| B. | 此粒子在M点的电势能大于在N点的电势能 | |
| C. | 此粒子在M点的动能大于在N点的动能 | |
| D. | 电场中M点的电势高于N点的电势 |
| A. | 它将导致实验者测量的相邻计数点之间的间隔变大,从而使测得的加速度偏大 | |
| B. | 它将导致实验者用公式vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$求得的各计数点对应的瞬时速度偏大,从而用v-t图象处理数据时导致测得的加速度偏大 | |
| C. | 它将导致实验者用公式vn=$\frac{{x}_{n}+{x}_{n+1}}{2T}$求得的各计数点对应的瞬时速度偏小,从而用v-t图象处理数据时导致测得的加速度偏小 | |
| D. | 用逐差法处理数据时,由于代入的T的数据偏小,从而导致测得的加速度偏大 |
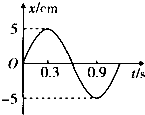
| A. | 0~O.3s | B. | 0~O.6s | C. | 0.6~O.9s | D. | 0.9~1.2s |
| A. | 向心加速度的方向始终与速度的方向垂直 | |
| B. | 向心加速度的方向保持不变 | |
| C. | 在匀速圆周运动中,向心加速度的方向保持不变 | |
| D. | 在匀速圆周运动中,向心加速度的大小保持不变 |
| A. | 加速时做正功,匀速时不做功,减速时做负功 | |
| B. | 加速时做正功,匀速和减速时做负功 | |
| C. | 加速和匀速做正功,减速时做负功 | |
| D. | 始终做正功 |
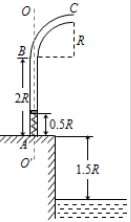 如图为某种鱼饵自动投放器中的投饵管装置示意图,上半部BC是半径为R的四分之一圆弧弯管,管口C处的切线沿水平方向,其下半部AB是一长为2R的竖直细管,AB管内有一原长为R、下端固定的轻质弹簧.投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上端放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去.设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零.不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g.求:
如图为某种鱼饵自动投放器中的投饵管装置示意图,上半部BC是半径为R的四分之一圆弧弯管,管口C处的切线沿水平方向,其下半部AB是一长为2R的竖直细管,AB管内有一原长为R、下端固定的轻质弹簧.投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上端放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去.设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零.不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g.求: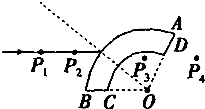 某兴趣实验小组利用一环形玻璃砖测定玻璃折射率的实验时,将玻璃砖平放在白纸上,在玻璃砖的外侧竖直插上两枚大头针P1、P2,然后在玻璃砖的内侧观察,调整视线使P2的像挡住P1的像.接着在内侧插两枚大头针P3和P4,使P3挡住P1和P2的像,P4挡住P3及P1和P2的像.然后在纸上标出大头针的位置以及环形玻璃砖的轮廓,如图,0为两圆弧圆心,图中画出了P1P2点的连线.
某兴趣实验小组利用一环形玻璃砖测定玻璃折射率的实验时,将玻璃砖平放在白纸上,在玻璃砖的外侧竖直插上两枚大头针P1、P2,然后在玻璃砖的内侧观察,调整视线使P2的像挡住P1的像.接着在内侧插两枚大头针P3和P4,使P3挡住P1和P2的像,P4挡住P3及P1和P2的像.然后在纸上标出大头针的位置以及环形玻璃砖的轮廓,如图,0为两圆弧圆心,图中画出了P1P2点的连线.