题目内容
9. 一同学在半径为1m的光滑圆弧面内做测定重力加速度的实验(如图所示).他用一个直径为0.02m质量分布均匀的光滑实心球.操作步骤如下:
一同学在半径为1m的光滑圆弧面内做测定重力加速度的实验(如图所示).他用一个直径为0.02m质量分布均匀的光滑实心球.操作步骤如下:①将小球从槽中接近最低处(虚线)静止释放;
②测量多次全振动的时间并准确求出周期;
③将圆弧面半径作为摆长和周期代入单摆周期公式求出重力加速度.
则他在以上操作中应该改正的操作步骤是③(填写步骤序号);若不改正,测量所得的重力加速度的值与真实值相比会偏大(选填“偏大”或“偏小”).
分析 实际摆长是悬点到球心的距离,根据单摆周期公式导出的公式$g=\frac{4{π}^{2}L}{{T}^{2}}$分析误差;
解答 解:实际摆长是悬点到球心的距离,故计算摆长时应该用圆弧面半径R减去球的半径r;
根据单摆周期公式$T=2π\sqrt{\frac{L}{g}}$得:$g=\frac{4{π}^{2}L}{{T}^{2}}$,实际摆球摆动过程中,摆长测量值偏大,故重力加速度的测量值也偏大;
故答案为:③,偏大
点评 本题考查用单摆测量重力加速度,解答的关键是明确实验原理,知道误差来源.

练习册系列答案
相关题目
4. 如图所示,理想变压器的副线圈上通过较长的输电线接有两个相同的灯泡L1和L2.原线圈两端电压不变,输电线的等效电阻为R.开始时,开关S断开,当S接通后,下列说法正确的是( )
如图所示,理想变压器的副线圈上通过较长的输电线接有两个相同的灯泡L1和L2.原线圈两端电压不变,输电线的等效电阻为R.开始时,开关S断开,当S接通后,下列说法正确的是( )
 如图所示,理想变压器的副线圈上通过较长的输电线接有两个相同的灯泡L1和L2.原线圈两端电压不变,输电线的等效电阻为R.开始时,开关S断开,当S接通后,下列说法正确的是( )
如图所示,理想变压器的副线圈上通过较长的输电线接有两个相同的灯泡L1和L2.原线圈两端电压不变,输电线的等效电阻为R.开始时,开关S断开,当S接通后,下列说法正确的是( )| A. | 副线圈两端MN的输出电压减小 | B. | 输电线等效电阻R上的电压减小 | ||
| C. | 通过灯泡L1的电流减小 | D. | 原线圈中的电流减小 |
2.图1中所示装置可以用来测量硬弹簧(即劲度系数较大的弹簧)的劲度系数k.电源的电动势为E,内阻可忽略不计;滑动变阻器全长为l,重力加速度为g,V为理想电压表.当木板上没有放重物时,动变阻器的触头位于图1中a点,此时电压表示数为零.在木板上放置质量为m的重物,滑动变阻器的触头随木板一起下移.由电压表的示数U及其它给定条件,可计算出弹簧的劲度系数k.
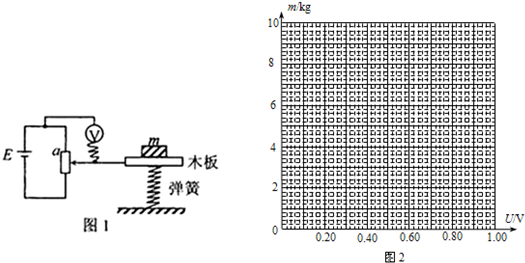
(1)写出m、U与k之间所满足的关系式.$m=\frac{lk}{Eg}U$
(2)己知E=1.50V,l=12.0cm,g=9.80m/s2.测量结果如表:
①在图2中给出的坐标纸上利用表中数据描出m-U直线.
②m-U直线的斜率为10.0kg/V.
③弹簧的劲度系数k=1.24×103N/m.(保留3位有效数字)

(1)写出m、U与k之间所满足的关系式.$m=\frac{lk}{Eg}U$
(2)己知E=1.50V,l=12.0cm,g=9.80m/s2.测量结果如表:
| m(kg) | 1.00 | 1.50 | 3.00 | 4.50 | 6.00 | 7.50 |
| U(V) | 0.108 | 0.154 | 0.290 | 0.446 | 0.608 | 0.740 |
②m-U直线的斜率为10.0kg/V.
③弹簧的劲度系数k=1.24×103N/m.(保留3位有效数字)
4. 如图所示,在光滑的水平地面上有一个表面光滑的物块P,它的质量为M,一长为L的轻杆下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个可视为质点的小球Q,它的质量为m,且M=5m.开始时,小球斜靠在物块左侧,它距地面的高度为h,物块右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )
如图所示,在光滑的水平地面上有一个表面光滑的物块P,它的质量为M,一长为L的轻杆下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个可视为质点的小球Q,它的质量为m,且M=5m.开始时,小球斜靠在物块左侧,它距地面的高度为h,物块右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )
 如图所示,在光滑的水平地面上有一个表面光滑的物块P,它的质量为M,一长为L的轻杆下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个可视为质点的小球Q,它的质量为m,且M=5m.开始时,小球斜靠在物块左侧,它距地面的高度为h,物块右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )
如图所示,在光滑的水平地面上有一个表面光滑的物块P,它的质量为M,一长为L的轻杆下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个可视为质点的小球Q,它的质量为m,且M=5m.开始时,小球斜靠在物块左侧,它距地面的高度为h,物块右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )| A. | 物块先做匀加速运动,后做匀速运动 | |
| B. | 在小球和物块分离前,当轻杆与水平面的夹角为θ时,小球的速度大小$\sqrt{\frac{2g(h-Lsinθ)}{{1+5si{n^2}θ}}}$ | |
| C. | 小球与物块分离时,小球一定只受重力作用 | |
| D. | 在小球落地之前,小球的机械能一直减少 |
14. 沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,M为介质中的一个质点,该波的传播速度为40m/s,则t=$\frac{1}{40}$s时( )
沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,M为介质中的一个质点,该波的传播速度为40m/s,则t=$\frac{1}{40}$s时( )
 沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,M为介质中的一个质点,该波的传播速度为40m/s,则t=$\frac{1}{40}$s时( )
沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,M为介质中的一个质点,该波的传播速度为40m/s,则t=$\frac{1}{40}$s时( )| A. | 质点M对平衡位置的位移一定为负值 | |
| B. | 质点M的速度方向与对平衡位置的位移方向相同 | |
| C. | 质点M的加速度方向与速度方向一定相同 | |
| D. | 质点M的回复力方向与对平衡位置的位移方向相同 |
1.某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.

(1)试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入表(保留3位有效数字)
(2)画出小车的瞬时速度随时间变化的关系图线.
(3)由所画速度-时间图象求出小车加速度为0.800 m/s2.

(1)试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入表(保留3位有效数字)
| VB | VC | VD | VE | VF | |
| 数值(m/s) | 0.400 | 0.479 | 0.560 | 0.640 | 0.721 |
(3)由所画速度-时间图象求出小车加速度为0.800 m/s2.
18.质量为1kg的物体,在空中由静止开始自由落下,经4s落地,以下说法中不正确的是(g取10m/s2)( )
| A. | 前2s内小球的动能增量为200J | B. | 第2s内重力做功为125J | ||
| C. | 第2s末重力做功的瞬时功率为200W | D. | 4s内重力做功的平均功率为200W |
 如图为“研究电磁感应现象”的实验装置.
如图为“研究电磁感应现象”的实验装置.