题目内容
14. 如图所示,条形区域AA′、BB′中存在方向垂直于纸面向外的匀强磁场,磁感应强度B的大小为0.3T,AA′、BB′为磁场边界,它们相互平行,条形区域的长度足够长,宽度d=1m.一束带正电的某种粒子从AA′上的O点以大小不同的速度沿着与AA′成60°角方向射入磁场,当粒子的速度小于等于某一值v0时,粒子在磁场区域内的运动时间始终为$\frac{4π}{3}$×10-8s,不计粒子所受重力.
如图所示,条形区域AA′、BB′中存在方向垂直于纸面向外的匀强磁场,磁感应强度B的大小为0.3T,AA′、BB′为磁场边界,它们相互平行,条形区域的长度足够长,宽度d=1m.一束带正电的某种粒子从AA′上的O点以大小不同的速度沿着与AA′成60°角方向射入磁场,当粒子的速度小于等于某一值v0时,粒子在磁场区域内的运动时间始终为$\frac{4π}{3}$×10-8s,不计粒子所受重力.(1)求粒子的比荷$\frac{q}{m}$
(2)求速度v0的大小
(3)当粒子速度为v1时,刚好垂直边界BB′射出磁场,求速度v1的大小.
分析 根据圆周运动的周期公式结合t=$\frac{θ}{2π}$T解得粒子的比荷,应用洛伦兹力提供向心力解出粒子运动的半径表达式,结合数学关系式解得速度.
解答 解:(1)若粒子的速度小于某一值v0时,则粒子不能从BB′离开磁场区域,只能从AA′边离开,无论粒子速度大小,在磁场中运动的时间相同,轨迹如图所示(图中只画了一个粒子的轨迹).
粒子在磁场区域内做圆周运动的圆心角均为φ1=240°,运动时间:t0=$\frac{2}{3}$T,
粒子做圆周运动的周期:T=$\frac{2πm}{qB}$,
代入数据解得:$\frac{q}{m}$≈3.33×108C/kg
(2)当粒子速度为v0时,粒子在磁场内的运动轨迹刚好与BB′边界相切,此时有
R0+R0sin30°=d ①
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{{R}_{0}}$ ②
由①②解得:v0=6.67×107m/s
(3)当粒子速度为v1时,刚好垂直边界BB′射出磁场区域,此时轨迹所对圆心角φ2=30°,由R1sin30°=d ③
由牛顿第二定律得:qv1B=m$\frac{{v}_{1}^{2}}{{R}_{1}}$ ④
由③④解得:v1≈2×108m/s
答:(1)粒子的比荷$\frac{q}{m}$为3.33×108C/kg;
(2)速度v0为6.67×107m/s;
(3)速度v1为2×108m/s.
点评 本题解题的关键在于画出粒子运动轨迹,分析粒子圆周运动周期与磁场变化周期的关系.粒子圆周运动的时间往往根据轨迹的圆心角与周期的关系确定,t=$\frac{θ}{2π}$T,θ为转过的圆心角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.物体做匀加速直线运动,加速度为a,物体通过A点时的速度为vA,经过时间t到达B点,速度为vB,再经过时间t到达C点速度为vC,则有( )
| A. | vB=$\frac{{v}_{A}+{v}_{C}}{2}$ | B. | vB=$\frac{AB+BC}{t}$ | C. | a=$\frac{BC-AB}{{t}^{2}}$ | D. | a=$\frac{{v}_{C}+{v}_{A}}{2t}$ |
9. 某物体由静止开始运动,它所受到的合外力方向不变,大小随时间变化的规律如图所示,则在0~t0这段时间( )
某物体由静止开始运动,它所受到的合外力方向不变,大小随时间变化的规律如图所示,则在0~t0这段时间( )
 某物体由静止开始运动,它所受到的合外力方向不变,大小随时间变化的规律如图所示,则在0~t0这段时间( )
某物体由静止开始运动,它所受到的合外力方向不变,大小随时间变化的规律如图所示,则在0~t0这段时间( )| A. | 物体做匀加速直线运动 | |
| B. | 物体在t0时刻速度最小 | |
| C. | 物体在t0时刻加速度最大 | |
| D. | 物体作变加速运动,运动速度越越大 |
19.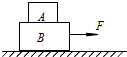 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )
 如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )
如图所示,物块A、B叠放在粗糙的水平桌面上,水平外力F作用在B上,使A、B一起沿水平桌面向右加速运动.设A、B之间的摩擦力为f1,B与水平桌面间的摩擦力为f2.在始终保持A、B相对静止的情况下,逐渐增大F则摩擦力f1和f2的大小( )| A. | f1不变、f2变大 | B. | f1变大、f2不变 | C. | f1和f2都变大 | D. | f1和f2都不变 |
3.关于运动和力下列说法正确的是( )
| A. | 当物体所受合外力不变时,运动状态是变化的 | |
| B. | 两个质量相同的物体,速度大不容易停下来,故速度大的惯性大 | |
| C. | 子弹从枪筒里打出以后能继续飞行是由于受到火药的推力作用 | |
| D. | 物体运动的速度越大,它所受的合外力一定越大 |

 如图所示,有一长为x=16m的水平传送带以v=10m/s的速度匀速运动,现将一物体轻轻放在传送带的左端,物体与传送带间的动摩擦因数为μ=0.5,则将物体被传送到右端所需时间为多少?(取g=10m/s2)
如图所示,有一长为x=16m的水平传送带以v=10m/s的速度匀速运动,现将一物体轻轻放在传送带的左端,物体与传送带间的动摩擦因数为μ=0.5,则将物体被传送到右端所需时间为多少?(取g=10m/s2)
