题目内容
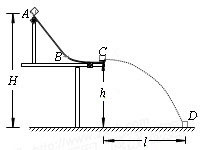
 如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑1/4圆形轨道,BC段为高h=5m的竖直轨道,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,离开B点做平抛运动(g取10m/s2),求:
如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑1/4圆形轨道,BC段为高h=5m的竖直轨道,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,离开B点做平抛运动(g取10m/s2),求:(1)小球到达B点时对圆形轨道的压力大小?
(2)如果在BCD轨道上放置一个倾角θ=45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果不能,请说明理由;如果能,请求出它第一次落在斜面上的位置.
分析:(1)小球在B点时做的是匀速圆周运动,对小球受力分析,由向心力的公式可以求得小球受到的支持力的大小,在根据牛顿第三定律可以知道对圆形轨道的压力大小;
(2)小球做平抛运动,根据平抛运动的规律可以求得水平距离,与斜面的长度相对比,可以知道,小球将落在斜面上,再根据平抛运动的规律可以求得落在斜面上的位置.
(2)小球做平抛运动,根据平抛运动的规律可以求得水平距离,与斜面的长度相对比,可以知道,小球将落在斜面上,再根据平抛运动的规律可以求得落在斜面上的位置.
解答:解:(1)小球在B处受重力G和向上的弹力F作用,由牛顿第二定律有:
F向=F-G=
,
解得:F=3N
由牛顿第三定律知球对B的压力F′=F,即小球到达B点时对圆形轨道的压力大小为3N,方向竖直向下.
(2)设小球离开B点做平抛运动的时间为t1,落地点到C点距离为s
由h=
gt12
得:t1=
=
s=1s,
则有:s=vBt1=2×1 m=2 m
如图,斜面BEC的倾角θ=45°,CE长d=h=5m,因为d>s,所以小球离开B点后能落在斜面上.(说明:其它解释合理的同样给分.)
假设小球第一次落在斜面上F点,BF长为L,小球从B点到F点的时间为t2
Lcosθ=vBt2…①
Lsinθ=
gt22…②
联立①、②两式得:
t2=0.4s;
L=
=
m=0.8
m=1.13m
说明:关于F点的位置,其它表达正确的同样也行.

答:(1)小球到达B点时对圆形轨道的压力大小为3N,方向向下;
(2)小球离开B点后能落到斜面上.它第一次落在斜面上的位置L=1.13m.
F向=F-G=
| mv2 |
| R |
解得:F=3N
由牛顿第三定律知球对B的压力F′=F,即小球到达B点时对圆形轨道的压力大小为3N,方向竖直向下.
(2)设小球离开B点做平抛运动的时间为t1,落地点到C点距离为s
由h=
| 1 |
| 2 |
得:t1=
|
|
则有:s=vBt1=2×1 m=2 m
如图,斜面BEC的倾角θ=45°,CE长d=h=5m,因为d>s,所以小球离开B点后能落在斜面上.(说明:其它解释合理的同样给分.)
假设小球第一次落在斜面上F点,BF长为L,小球从B点到F点的时间为t2
Lcosθ=vBt2…①
Lsinθ=
| 1 |
| 2 |
联立①、②两式得:
t2=0.4s;
L=
| vBt2 |
| cosθ |
| 2×0.4 | ||
|
| 2 |
说明:关于F点的位置,其它表达正确的同样也行.

答:(1)小球到达B点时对圆形轨道的压力大小为3N,方向向下;
(2)小球离开B点后能落到斜面上.它第一次落在斜面上的位置L=1.13m.
点评:本题考查了圆周运动和平抛运动的规律,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
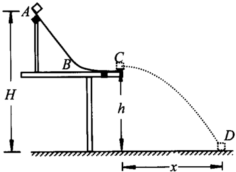 如图所示,轨道ABC被竖直地固定在水平桌面上,A距水平地面高H=0.75m,C距水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在地面上的D点.现测得C、D两点的水平距离为x=0.60m.不计空气阻力,取g=10m/s2.求
如图所示,轨道ABC被竖直地固定在水平桌面上,A距水平地面高H=0.75m,C距水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在地面上的D点.现测得C、D两点的水平距离为x=0.60m.不计空气阻力,取g=10m/s2.求
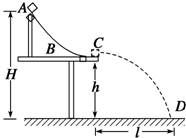 如图所示,轨道ABC被竖直地固定在水平桌面上,A距离水平地面高H=0.75m,C距离水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在水平地面上的D点.现测得C、D两点的水平距离为l=0.60m.不计空气阻力,取g=10m/s2.求:
如图所示,轨道ABC被竖直地固定在水平桌面上,A距离水平地面高H=0.75m,C距离水平地面高h=0.45m.一质量m=0.10kg的小物块自A点从静止开始下滑,从C点以水平速度飞出后落在水平地面上的D点.现测得C、D两点的水平距离为l=0.60m.不计空气阻力,取g=10m/s2.求: 如图所示,轨道ABC的AB是半径为0.4m的光滑
如图所示,轨道ABC的AB是半径为0.4m的光滑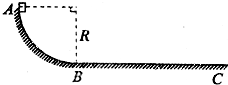 如图所示,轨道ABC的AB是半径为0.4m的光滑
如图所示,轨道ABC的AB是半径为0.4m的光滑